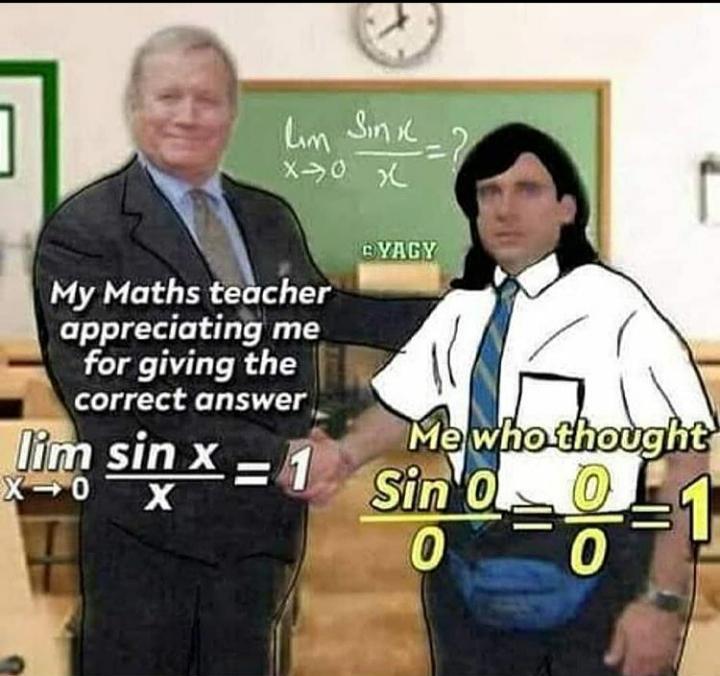L'Hôpital To The Rescue

That moment when you're staring at lim(sin x/x) as x approaches 0 and your brain short-circuits! The student thinks they're clever by directly plugging in x=0, getting sin(0)/0 = 0/0 = 1... which is mathematical blasphemy! That's an indeterminate form, you beautiful disaster!

Enter L'Hôpital's rule—the calculus superhero that swoops in when limits get messy. It transforms that 0/0 nightmare into a solvable derivative ratio. The correct approach gives us the limit = 1, but for completely different reasons than our confident-yet-confused friend imagined.

Every calculus professor has that internal scream when students accidentally get the right answer through catastrophically wrong methods. It's like finding the cure for cancer by mixing random chemicals because "they looked pretty together."