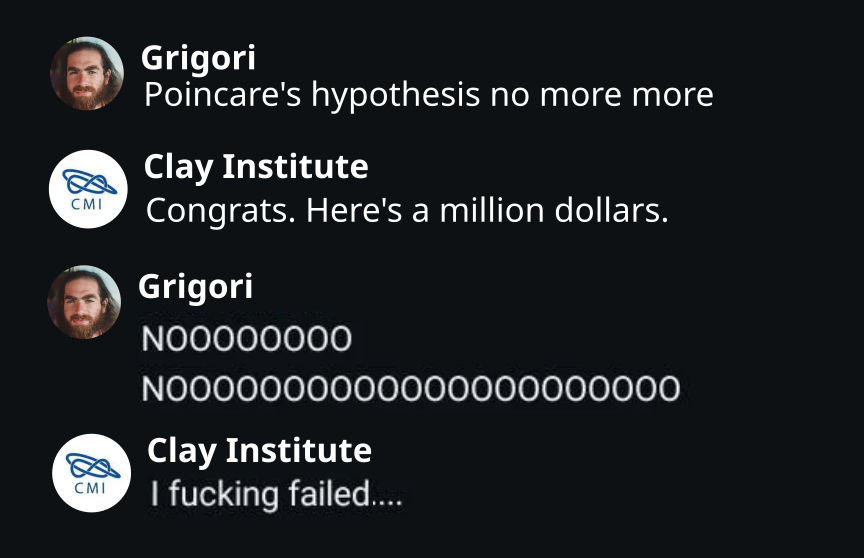
The famous red pill/blue pill scene has been repurposed for financial enlightenment! Choosing between $2 now or $1 that doubles daily is the ultimate test of delayed gratification and exponential growth understanding. Sure, $2 looks tempting (hello, vending machine snack!), but that self-multiplying dollar becomes $2 on day 2, $4 on day 3, $8 on day 4... By day 10, you're at $512. After 30 days? A cool $536,870,912! Even mathematicians get sweaty palms thinking about compound interest. The real scientific principle here is exponential growth - the same concept behind population explosions, viral spread, and why your lab bacteria culture suddenly took over the incubator overnight.


 Academia
Academia
 Ai
Ai
 Astronomy
Astronomy
 Biology
Biology
 Chemistry
Chemistry
 Climate
Climate
 Conspiracy
Conspiracy
 Earth-science
Earth-science
 Engineering
Engineering
 Evolution
Evolution
 Geology
Geology