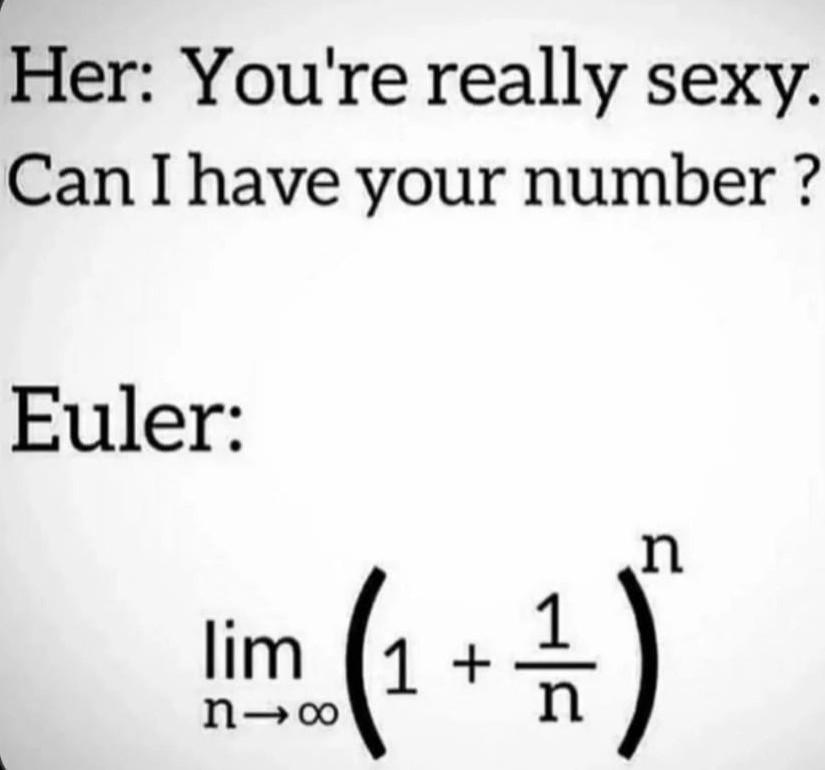The existential crisis that hits when you learn about Gödel's Incompleteness Theorem is too real! Suddenly you're questioning if your breakfast cereal choice is an unprovable statement within its axiomatic system.
For the uninitiated, Gödel basically shattered mathematics by proving that in any consistent formal system complex enough to express basic arithmetic, there will always exist true statements that cannot be proven within that system. So now you're pointing at literally everything going "Wait... is THAT unprovable too??"
Mathematical completeness? Sorry, it's just not on the menu. Your formal system is either inconsistent or incomplete. Pick your existential nightmare!

 Academia
Academia
 Ai
Ai
 Astronomy
Astronomy
 Biology
Biology
 Chemistry
Chemistry
 Climate
Climate
 Conspiracy
Conspiracy
 Earth-science
Earth-science
 Engineering
Engineering
 Evolution
Evolution
 Geology
Geology