Taylor series Memes

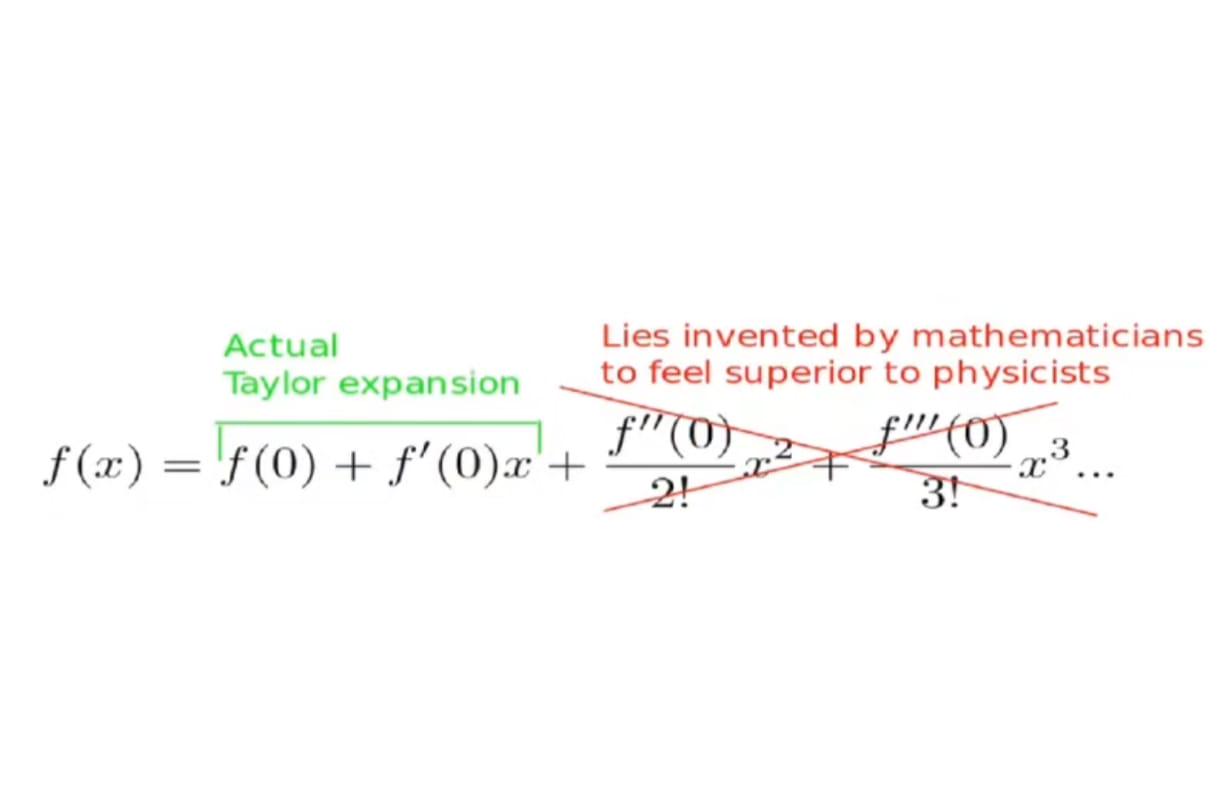
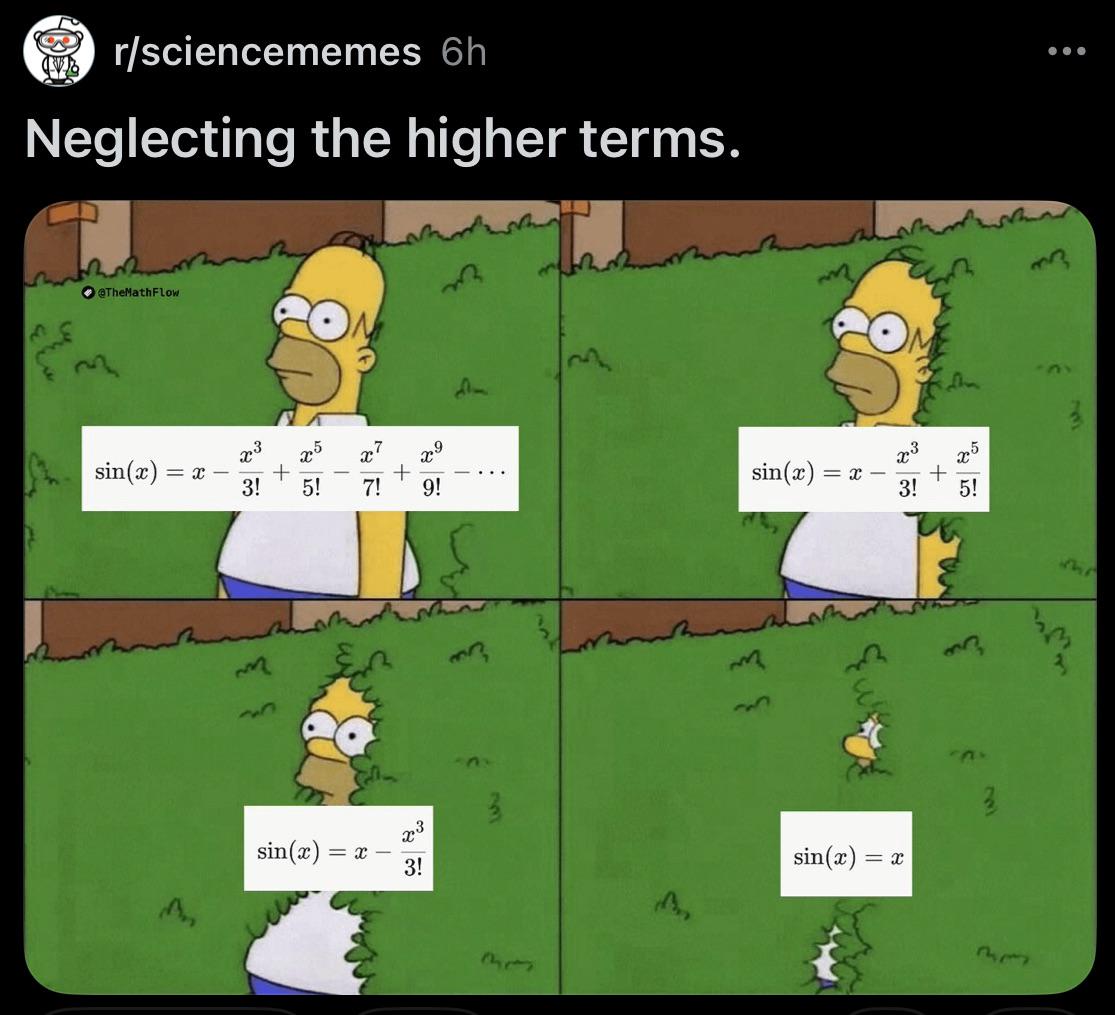
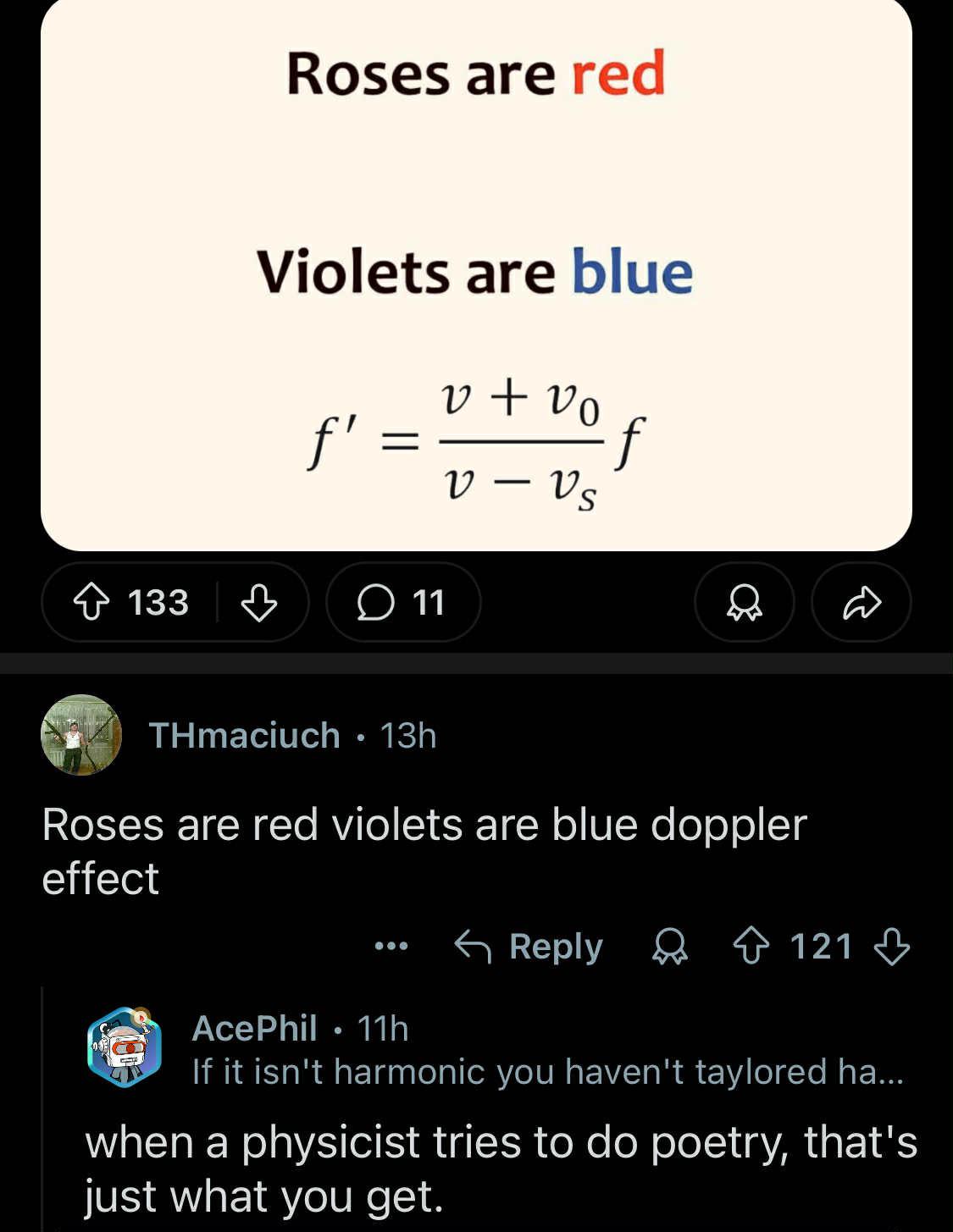
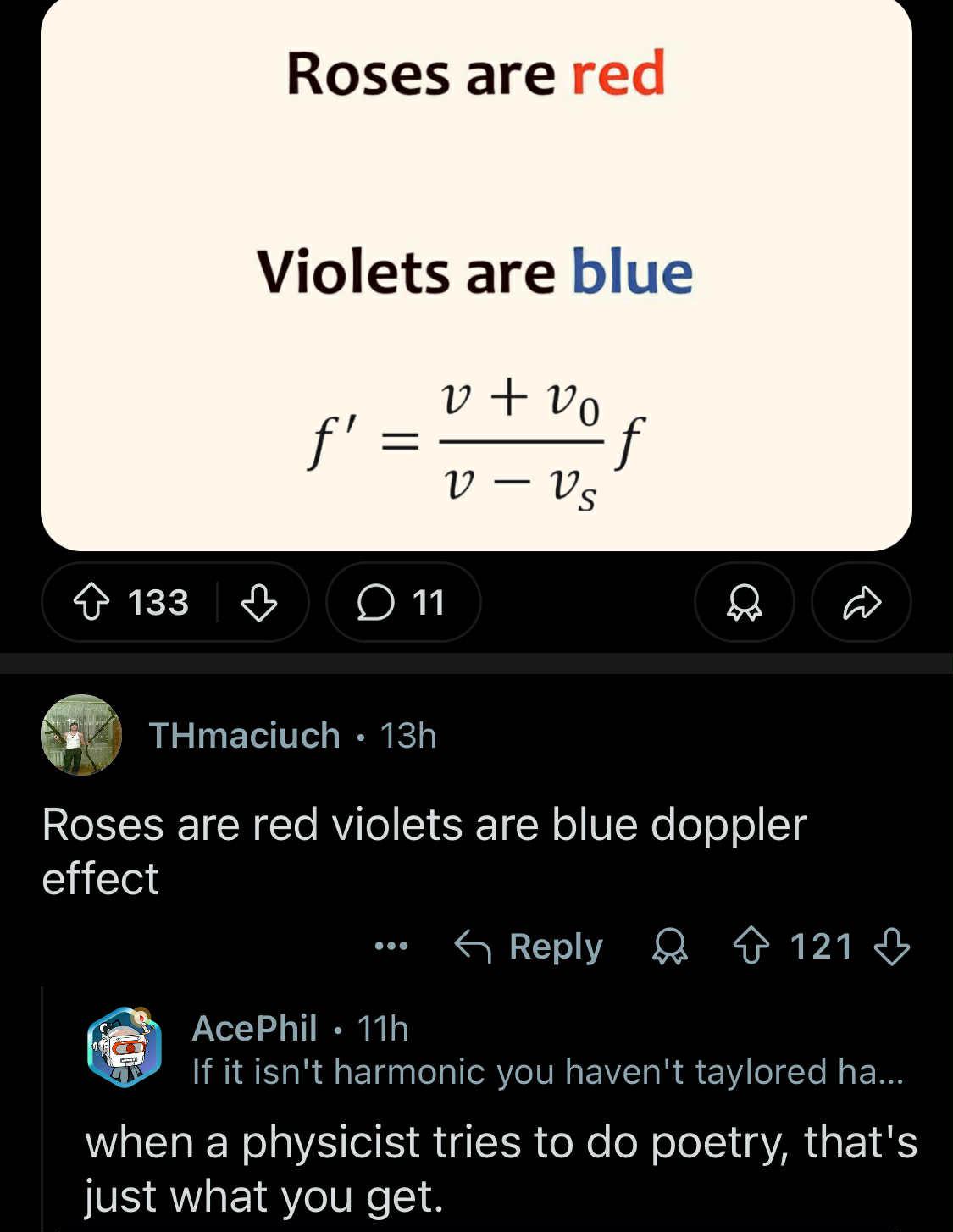
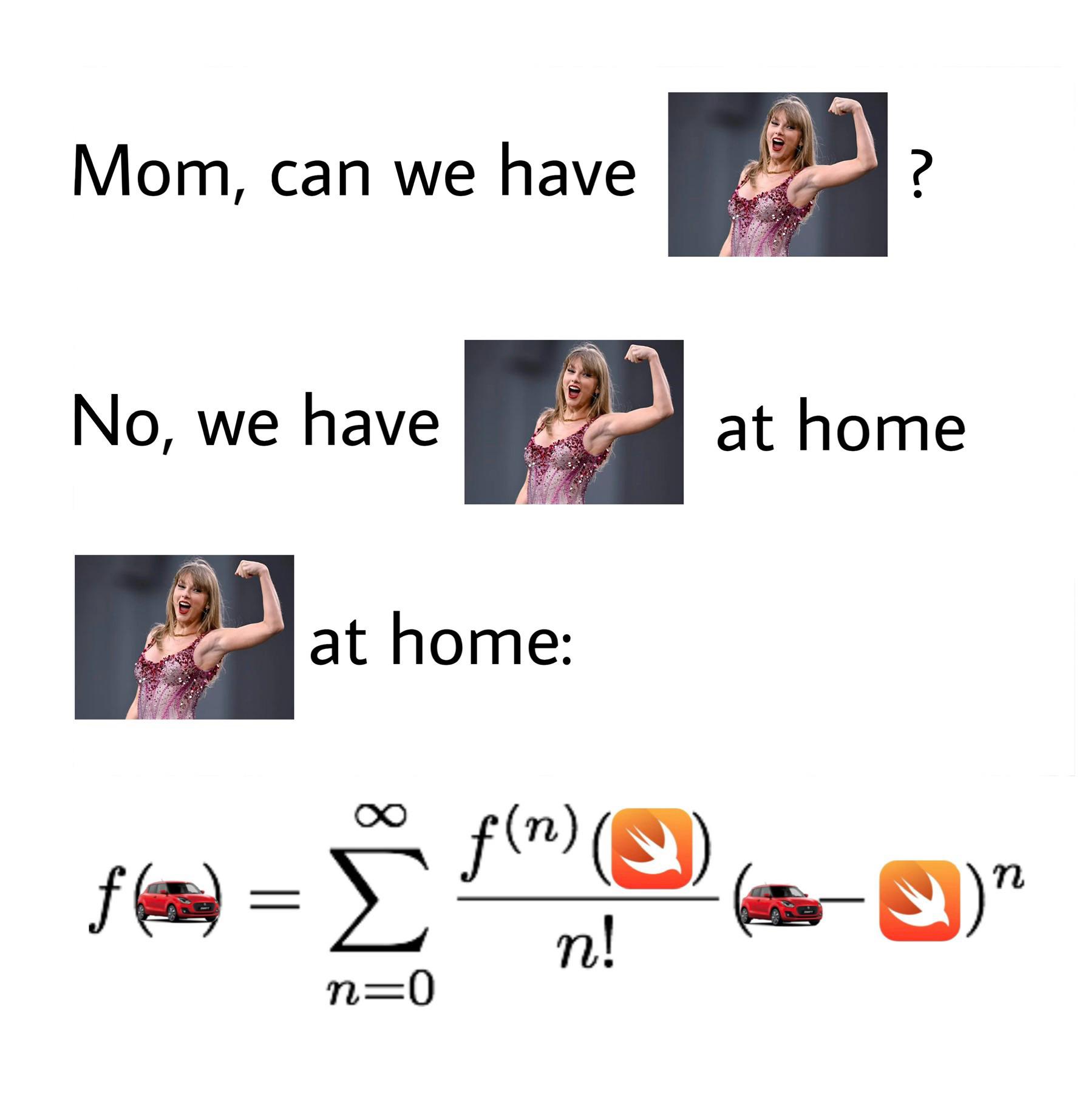Calculus nerds have found their ultimate crossover episode! The meme brilliantly pits pop star Taylor Swift against the mathematical Taylor Series, and the results are *infinitely* clear. While Swift might dominate the charts, she can't help you approximate sine functions or reduce those pesky nonlinear equations. Meanwhile, the Taylor Series is out here expanding functions around points like it's no big deal, showing up on your calculus exam, and training your analytical reasoning skills. The Taylor Series (that beautiful summation formula) lets mathematicians approximate complex functions using polynomials - basically the mathematical equivalent of having backup dancers make you look good. Just remember its effectiveness depends on the convergence range, unlike Swift's range which consistently hits those high notes. Next album idea: "Taylor's Version (Expanded Around a Point)"

The ultimate showdown for calculus nerds! While Taylor Swift dominates the music charts, the Taylor Series dominates engineering math by expanding functions around a point. Unlike the pop star, this mathematical powerhouse actually helps you approximate sin(x), reduces nonlinear equations, and is guaranteed to appear on your calculus exam. Math professors everywhere are nodding in approval while engineering students are frantically writing this formula on their cheat sheets. The convergence range might be limited, but hey, at least the Taylor Series trains your approximation skills—something no amount of Swiftie merchandise can do!

Engineers committing mathematical heresy by approximating sin(x) with just x - x³/6 is the kind of violence that keeps mathematicians up at night. The full Taylor series for sine contains infinite terms, but engineers just shrug and say "good enough for government work." Pure mathematicians witnessing this crime against calculus is like watching someone eat a five-course meal with their hands. The approximation works surprisingly well for small angles, which is exactly the kind of pragmatic shortcut that makes theoretical mathematicians clutch their chalk in horror.

The eternal rivalry between physicists and mathematicians captured in one equation! Physicists are notorious for approximating complex functions with just the first couple of terms of a Taylor series, treating those higher-order derivatives as unnecessary complications. Meanwhile, mathematicians clutch their pearls at such blasphemy. The truth? Most physical problems work perfectly fine with the simplified version because those tiny higher-order terms contribute about as much as my motivation on Monday mornings—effectively zero. Engineers are somewhere in the background, already using just f(0) and calling it "close enough for government work."

The mathematical gangsters have spoken! The Taylor series might look fancy with its arbitrary center point c , but real ones know the Maclaurin series is just Taylor centered at zero. It's like showing up to a party with your complicated friend who insists on giving directions from some random landmark instead of just saying "start from downtown." Pure mathematicians spend hours proving they're different, while applied mathematicians just substitute c =0 and get on with their lives. Next time someone tries to impress you with Taylor series, just hit 'em with "cool story, but my homies reduce to Maclaurin."

The mathematical walk of shame! This meme shows what happens when you're too lazy to write out the full Taylor series for sine. With each panel, Homer disappears further into the bushes as more terms get dropped from the expansion. For small angles, sin(x) ≈ x is actually a decent approximation, which is why engineers can get away with it. But mathematicians? They'd rather die than commit such blasphemy. The more terms you drop, the more your professor's respect for you vanishes—just like Homer into those bushes.

Behold the mathematical horror story in four panels! This is what happens when you get too aggressive with Taylor series approximations. With each term Homer drops from the sine function's infinite series, he slowly disappears into the hedge of mathematical inaccuracy! By the time he's reduced the glorious sine function to just "sin(x) = x", he's practically vanished into the mathematical void! It's the calculus equivalent of saying "eh, close enough" and then watching reality collapse around you. Every math professor just felt a disturbance in the force.

The ultimate math flex! On the left, you've got the Pythagorean theorem tattoo - clean, elegant, fits on a single line. Then there's the competition with a full arm dedicated to Taylor series expansions, Euler's formula, and basically an entire calculus textbook. Who needs muscles when you can flex with mathematical equations? The perfect example of "tell me you're a math major without telling me you're a math major." That exponential function tattoo is definitely an irrational decision!

When you ask for Swift but get a Taylor series instead! The meme brilliantly plays on the classic "Mom, can we have X? No, we have X at home" format, but with a mathematical twist. What you wanted was the pop star Taylor Swift, but what you got was the Taylor series expansion—a mathematical formula that approximates functions as an infinite sum of terms. The equation shown is literally how mathematicians "expand" functions around a point, breaking them down term by term. Even funnier is the Swift programming language logo thrown in there, creating a triple pun! Poor Maclaurin series (Taylor's special case where a=0) never gets the spotlight despite doing all the heavy lifting in calculus classes.

The eternal battle between pure mathematicians and physicists in one birdy showdown! 🐦 Physics majors are literally SCREAMING at the sight of pure math, while the mathematicians are busy chomping down on abstract concepts without a care for real-world applications. The physicist bird is having a meltdown over the lack of units, demanding more rigor, and complaining that Taylor series should have more than 3 terms (the AUDACITY!). But then... the enlightenment! That "WOW" moment when physicists finally grasp the elegant beauty of mathematics. From rage to bubbles of pure thought - the transformation is *chef's kiss* magnificent! 💭 Every physicist eventually realizes that π = 3 and e = 2 are perfectly reasonable approximations... until your bridge collapses! 🌉💥