Ad LG 34" Curved UltraWide
So wide your spreadsheets need a passport

Each purchase brings us closer to affording that AI that turns grant applications into actual funding. 🤖

 Academia
Academia
 Ai
Ai
 Astronomy
Astronomy
 Biology
Biology
 Chemistry
Chemistry
 Climate
Climate
 Conspiracy
Conspiracy
 Earth-science
Earth-science
 Engineering
Engineering
 Evolution
Evolution
 Geology
Geology
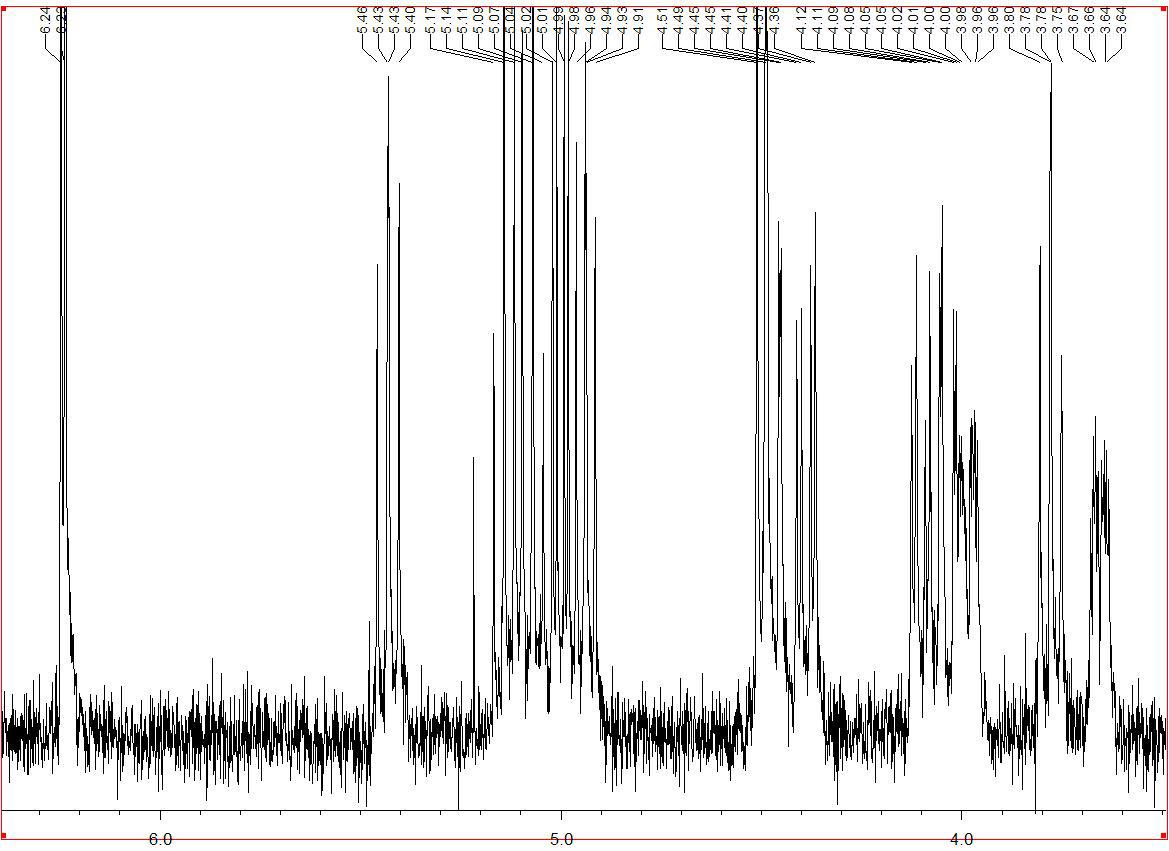
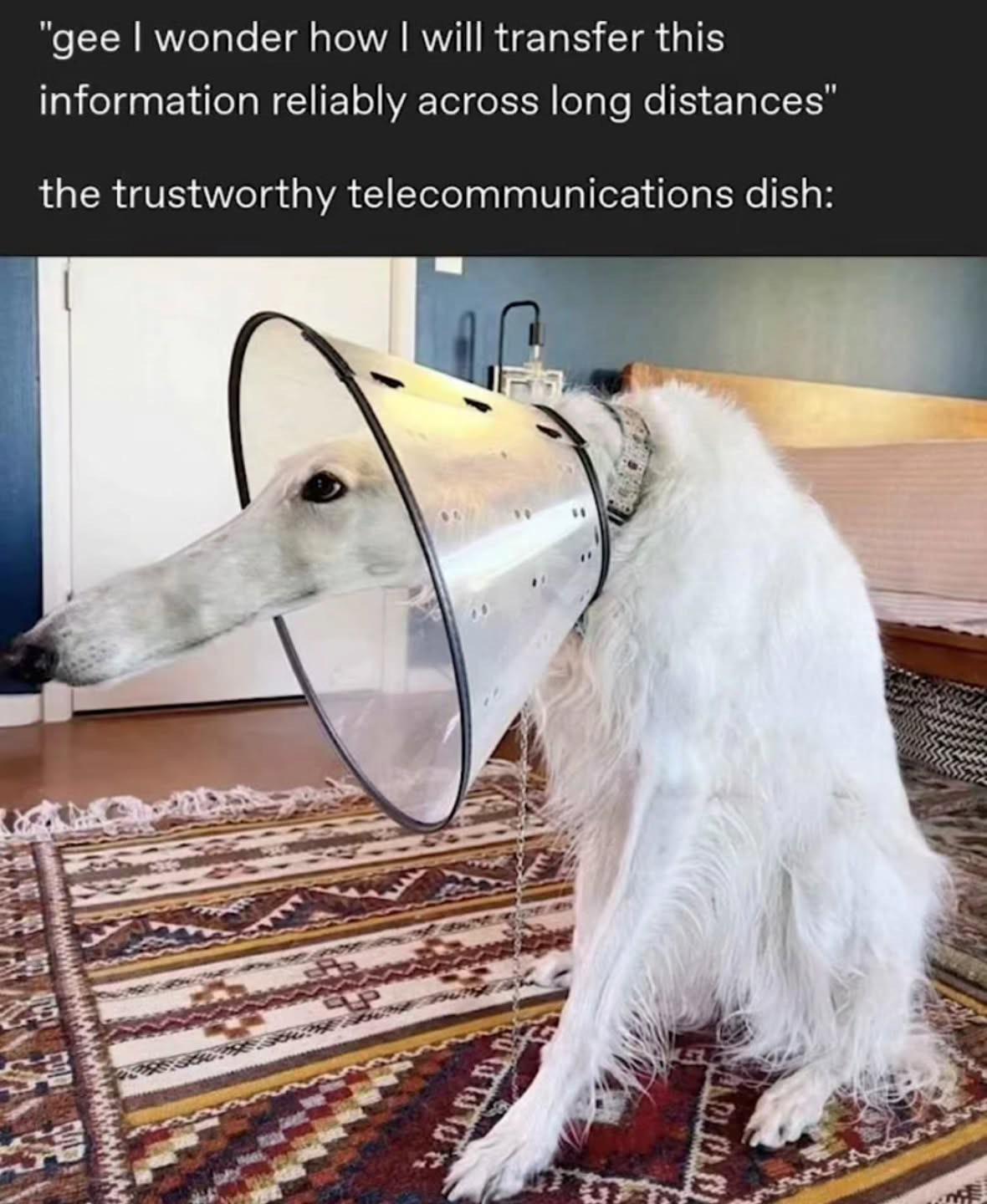

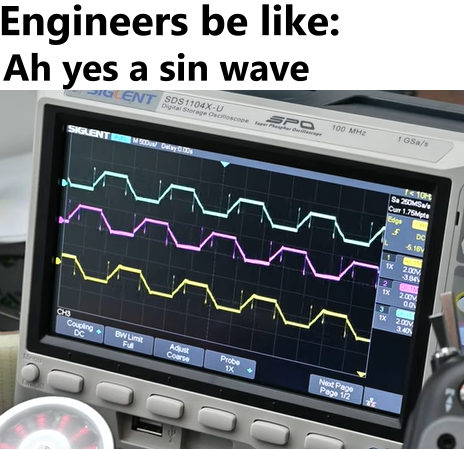




![Still Si[Ng]Le: Engineering Solutions To Dating Problems](https://i.sciencehumor.io/2025/03/f77f343ba3b79c043020cccd260ace1c943db67a5c2feb1d22313b0443ebc660.jpeg)
