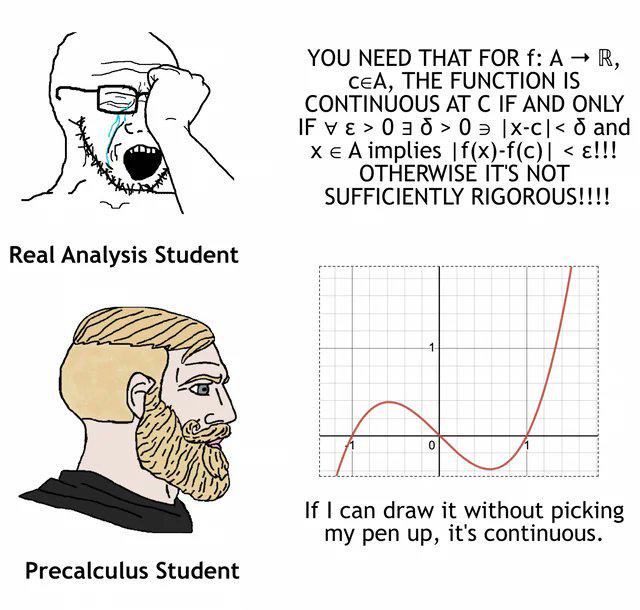
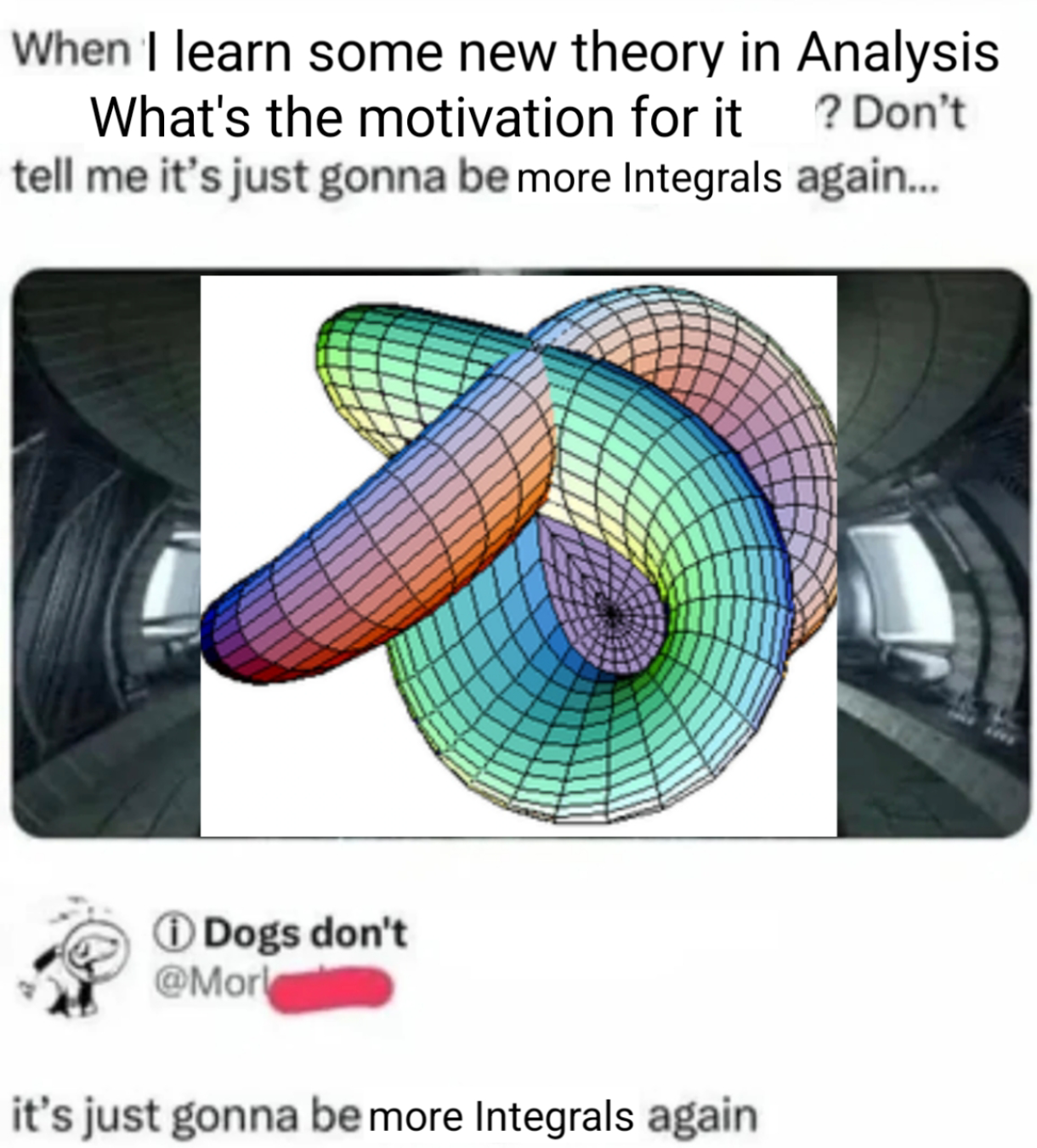
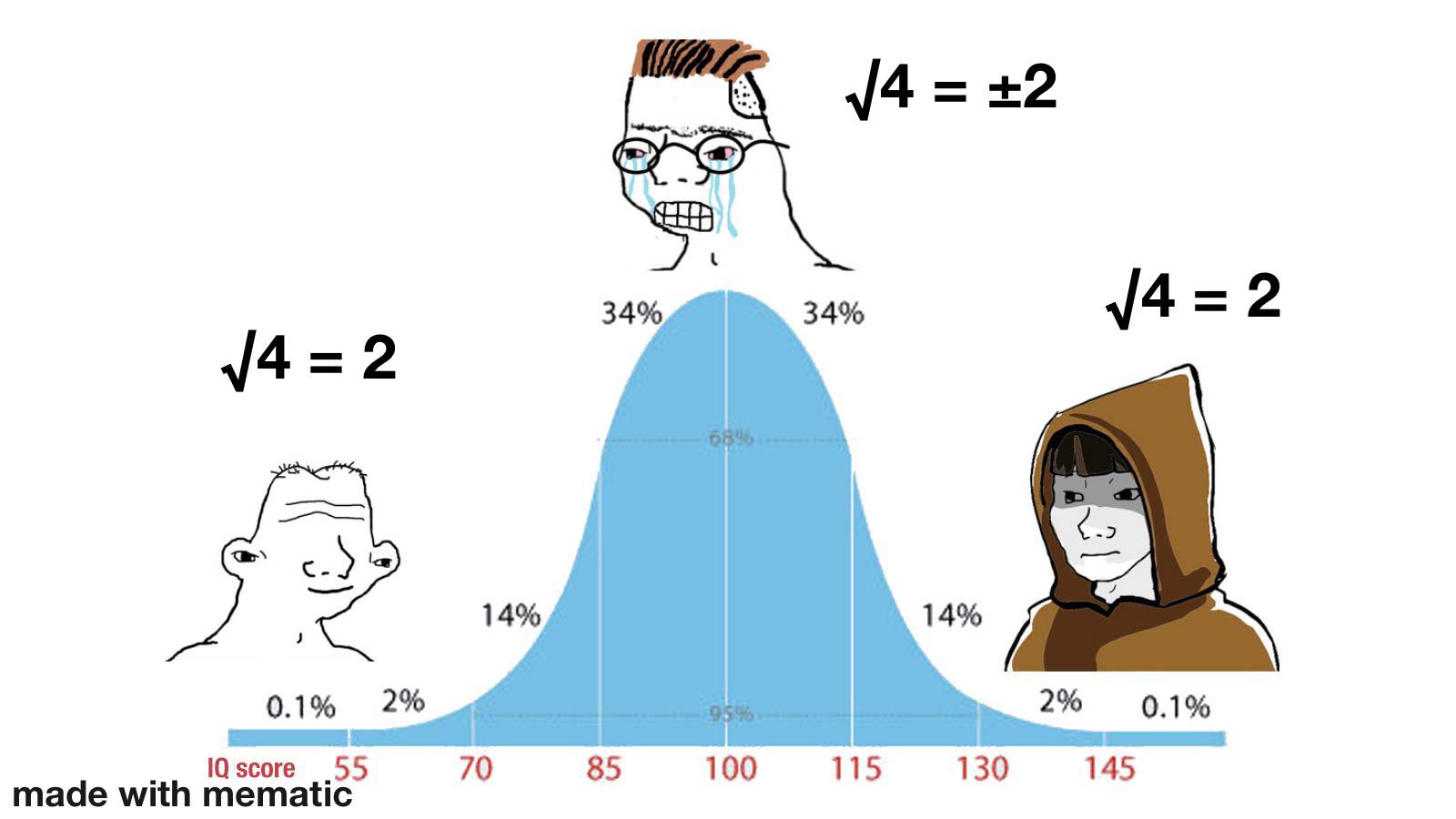
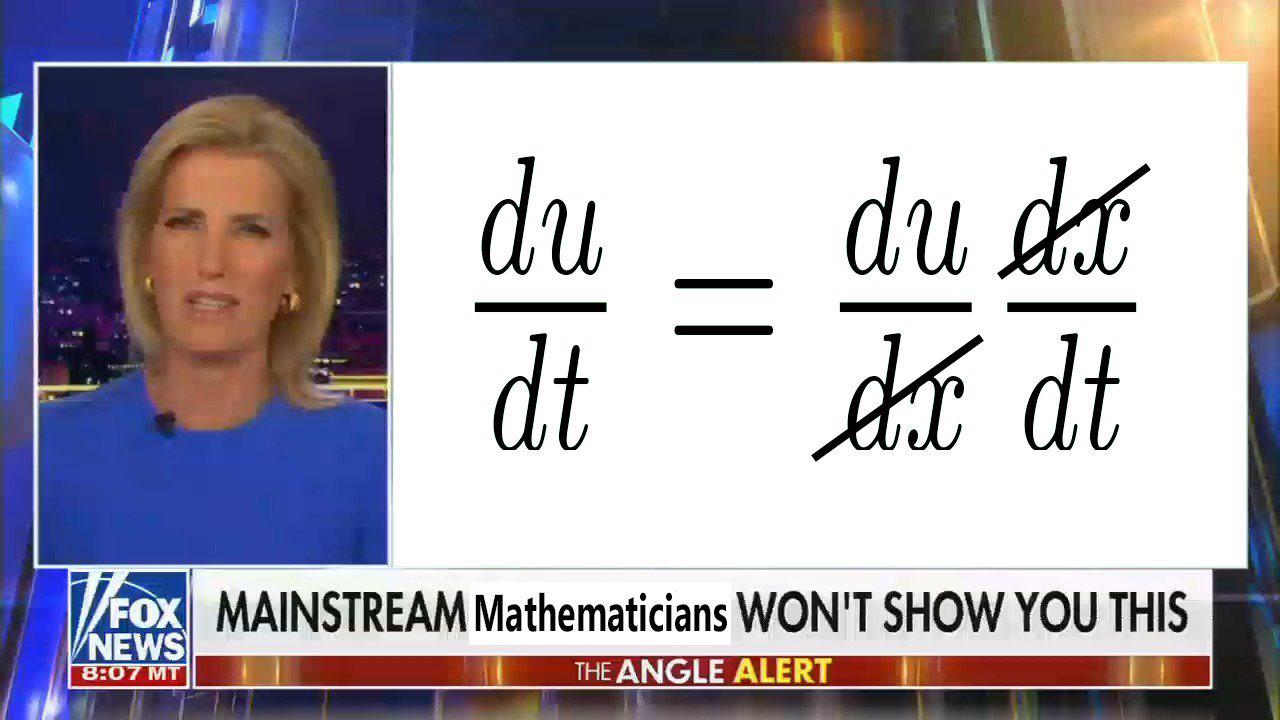Ever notice how textbooks present complex math like it's a casual stroll through a park? Meanwhile, underneath that serene landscape, generations of mathematicians fought bloody battles with notation, proofs, and existential crises. That elegant equation you're skimming over? Some poor soul probably sacrificed their marriage, sanity, and vitamin D levels to discover it. Next time you casually flip through Calculus, pour one out for Newton, who spent years in plague-induced isolation developing it while the rest of England was busy not inventing calculus. Trust me, behind every "trivial proof" is a mathematician who once cried at 3 AM surrounded by crumpled papers and broken dreams.


 Academia
Academia
 Ai
Ai
 Astronomy
Astronomy
 Biology
Biology
 Chemistry
Chemistry
 Climate
Climate
 Conspiracy
Conspiracy
 Earth-science
Earth-science
 Engineering
Engineering
 Evolution
Evolution
 Geology
Geology