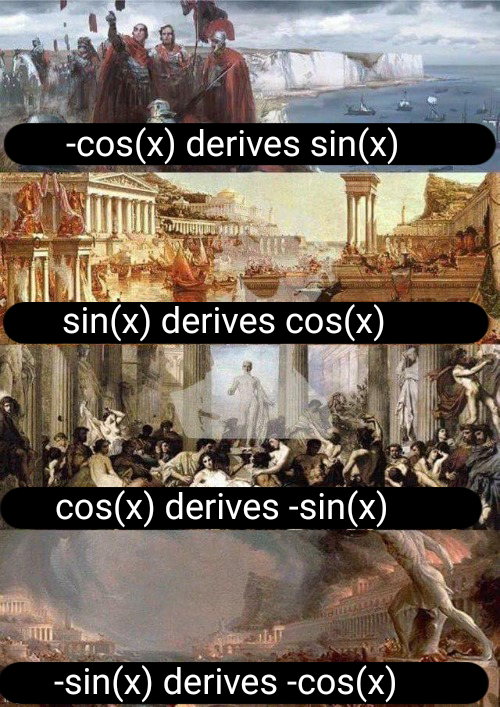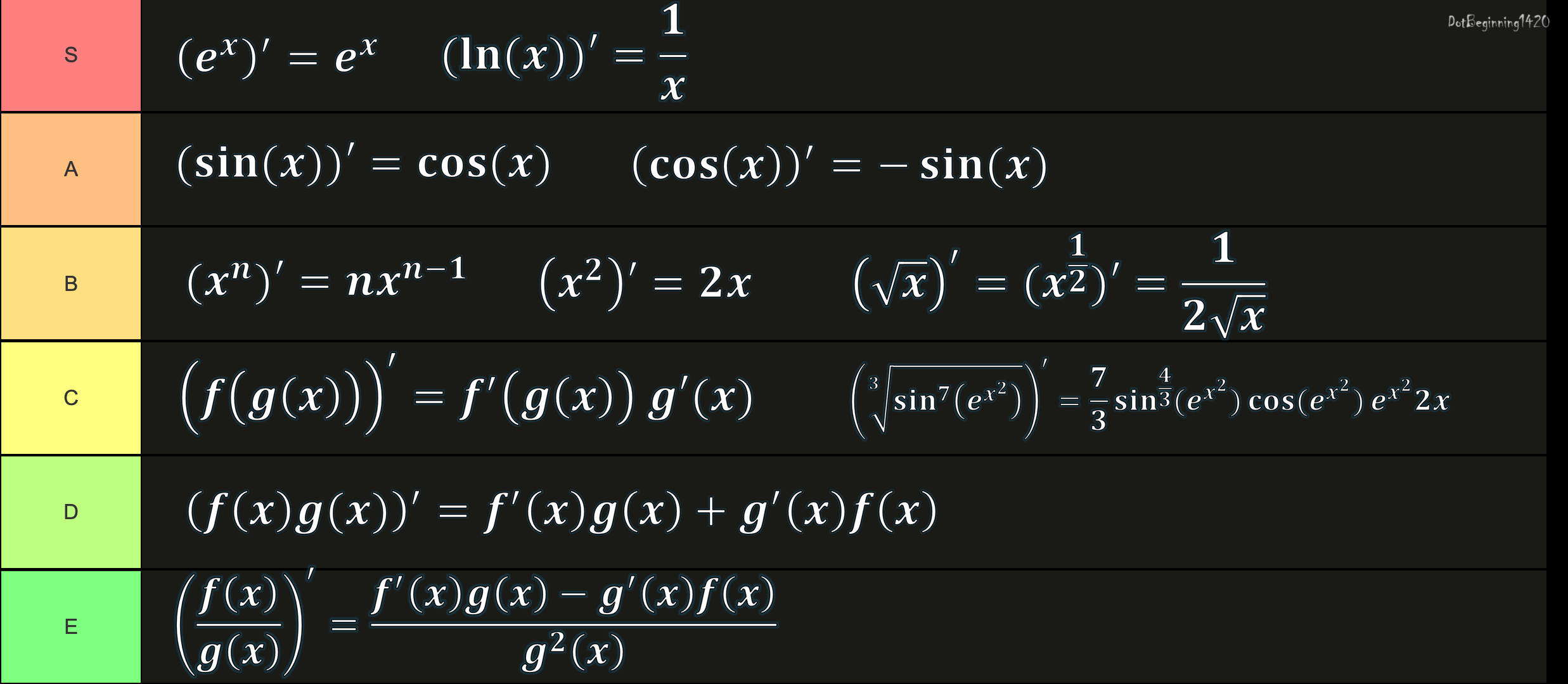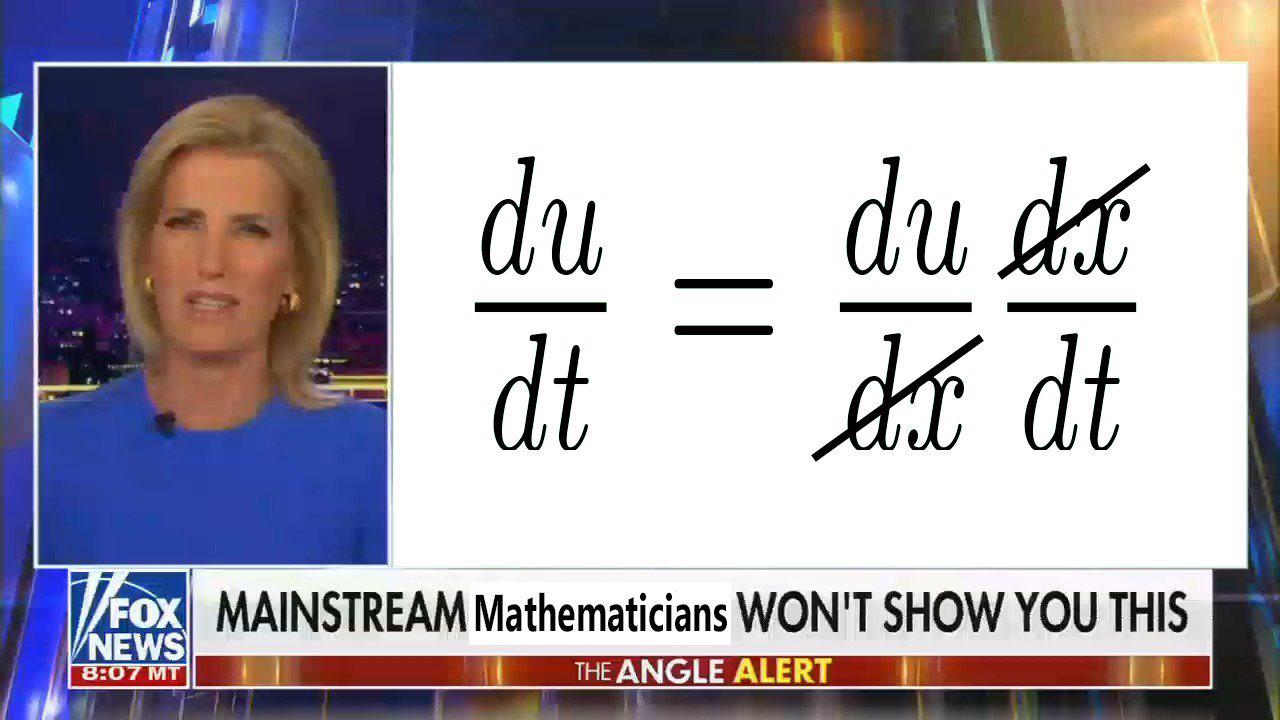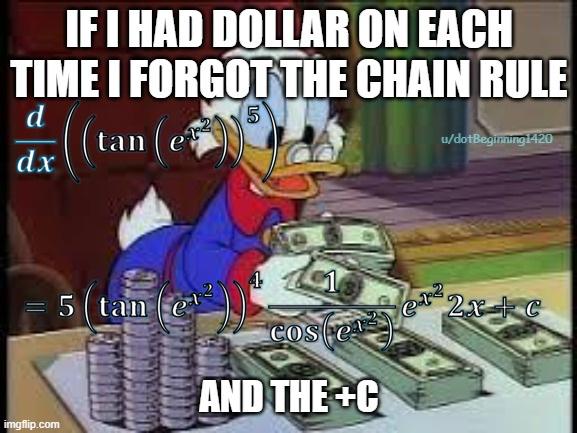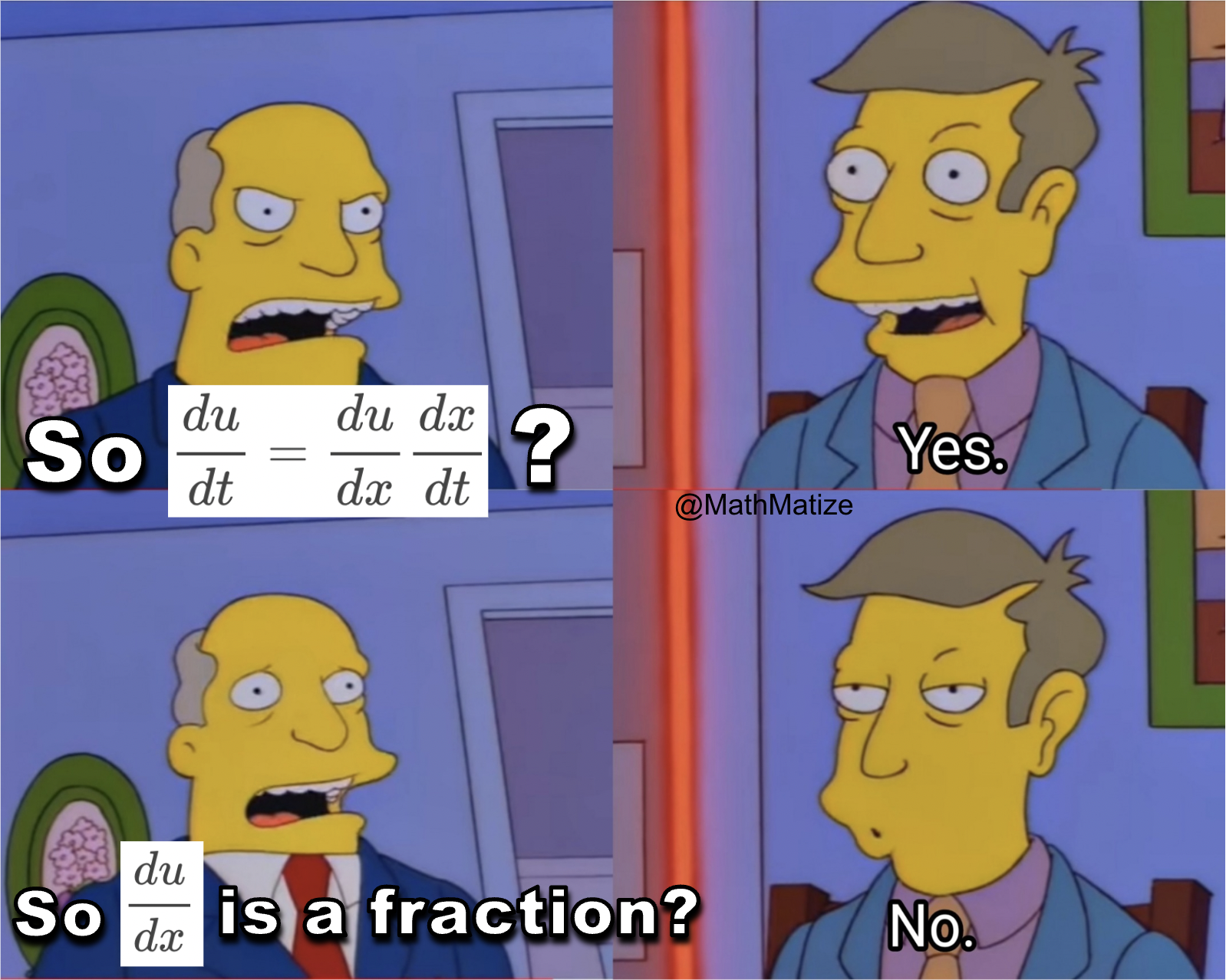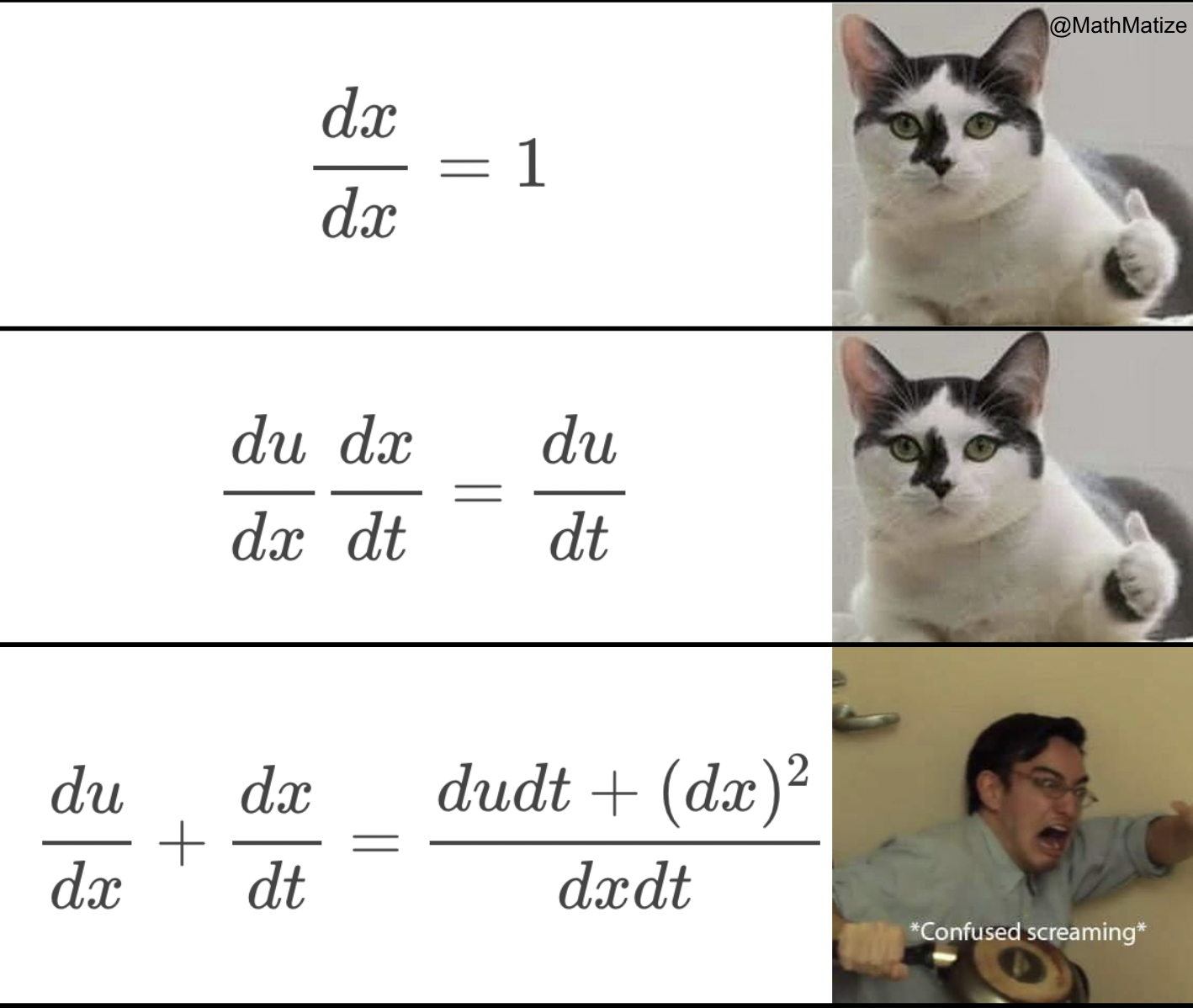Chain rule Memes

The calculus gatekeepers have spoken! At the top, we have the elegant definition of differentiation—a beautiful limit that captures the essence of instantaneous change. Below that? The chaotic battlefield where mathematicians store their emotional trauma. Every time you memorize a derivative formula instead of deriving it from first principles, a mathematician somewhere sheds a single tear. Sure, you could painfully work through the chain rule from scratch every time... or you could just accept that these formulas are the mathematical equivalent of therapy. Remember kids, real mathematicians derive everything from scratch—and also never sleep, subsist entirely on coffee, and have "lim h→0" tattooed somewhere inappropriate.

The eternal calculus paradox that haunts undergrads everywhere. First, the professor confidently states that du/dt = (du/dx)(dx/dt), treating du/dx like a perfectly normal fraction. Then when a student dares to ask if du/dx is actually a fraction, suddenly it's "No." Welcome to mathematics, where we use fraction notation for things that aren't fractions, cancel terms that technically can't be canceled, and somehow still get the right answer. Schrödinger's fraction—simultaneously a fraction and not a fraction until a student asks about it.

This is calculus escalation at its finest! The first panel shows a cat calmly accepting the trivial identity dx/dx = 1. The second panel? Still cool with the chain rule simplification. But that third panel—where differential algebra goes completely bonkers with terms flying everywhere—triggers pure mathematical hysteria. It's like watching someone peacefully solving basic equations until suddenly they're thrown into the differential equation thunderdome. The perfect visualization of that moment when your professor says "this is just a simple application" and then writes something that looks like it summoned a math demon.

The mathematical evolution no one asked for but everyone needed. First panel: innocent Calc 1 student being introduced to the chain rule with the basic formula. Middle panel: the rigorous proof that makes students question their life choices. Final panel: the chad Applied Analysis enjoyer who's transcended formalities and just writes it as a ratio of differentials without breaking a sweat. Nothing says "I've suffered enough" like skipping all the epsilon-delta nonsense and getting straight to the point. The chain rule—traumatizing undergrads since calculus was invented.

The eternal struggle of calculus students everywhere! Someone claims they've found the chain rule for integration (which doesn't exist because integration requires techniques like substitution, not a simple formula). Then—poof—[removed]. Just like that, mathematical salvation yanked away. It's the academic equivalent of "I know the secret to eternal life but oops, dropped my notes in a volcano." Every generation of math students falls for this cruel joke, desperately clicking only to find the promised land remains forever out of reach.

The moment you realize the chain rule is just a fancy way of saying "derivatives can party like fractions" and your entire calculus worldview shifts! That sudden 5 AM epiphany where dp/dt = dp/dx * dx/dt looks suspiciously like fractions canceling out (even though technically they're not). Math professors everywhere are both proud and slightly concerned about your sleep schedule. The chain rule - secretly just fraction manipulation in a trench coat this whole time!

Nothing triggers a calculus professor faster than canceling differentials like they're fractions. That equation showing dy/du · du/dx = dy/dx is mathematically correct but for entirely different reasons than "the du's cancel out." It's the chain rule in disguise, not some algebraic simplification. Professors everywhere clutch their chalk in horror when students cross out the differentials like they're solving for x in 8th grade algebra. Pure mathematical blasphemy.

The eternal struggle of the calculus novice. Looking at the chain rule formula and mistaking those differential notations for simple fractions you can cancel out. The mathematical equivalent of thinking you can just delete the denominators because they look the same. Every calculus professor just felt a disturbance in the force.

When you're a physics student trying to survive calculus with mathematical blasphemy! The derivative notation dy/dx isn't technically a fraction, but treating it like one sometimes gives correct answers through a mathematical miracle called the "chain rule." Calculus teachers watching physics students divide these symbols like fractions be like: *internal screaming intensifies* But hey, if it gets you through your physics exam without summoning a black hole, who's complaining?

That moment when calculus suddenly makes sense and your entire worldview shatters! The chain rule isn't just mathematical torture—it's actually useful ?! The textbook casually explains you can cancel out derivatives like they're fractions, and suddenly years of your math teacher screaming "DERIVATIVES ARE NOT FRACTIONS" comes flooding back. Your brain short-circuits as you realize they've been secretly canceling dx terms this whole time while pretending to be rigorous. It's like finding out your parents have been sneaking vegetables into your dessert for decades. The mathematical betrayal is REAL!