Academia
Ai
Astronomy
Biology
Chemistry
Climate
Conspiracy
Earth-science
Engineering
Evolution
Geology
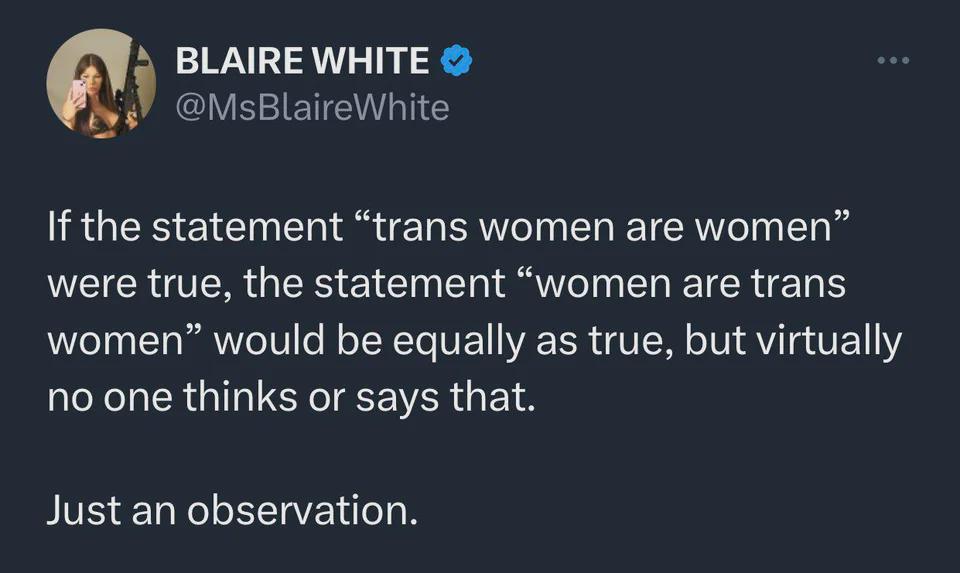
This is a classic case of someone trying to apply mathematical set theory to social concepts without understanding how logical implications actually work! The notation in the title (A ⊇ B ⇒ A ⊆ B) is mathematically incorrect - if A contains B (superset), it doesn't imply that A is contained in B (subset). That's like saying "if all squares are rectangles, then all rectangles are squares" - which is demonstrably false!
The tweet confuses subset relationships with categorical statements. In set theory, "trans women are women" would be expressed as "trans women ⊆ women" (trans women are a subset of women), but that doesn't logically imply the reverse statement "women ⊆ trans women" (all women are trans women).
The person clearly slept through their discrete mathematics class and now thinks they've made some profound logical discovery. Next time, bring coffee to those 8 AM math lectures!
