Set theory Memes

When your basketball GOAT debate meets discrete mathematics! The meme shows LeBron James facepalming because he committed the cardinal sin of mathematical logic—assuming transitivity where it doesn't apply. In basketball debates, fans love arguing "Player A beat Player B, who beat Player C, so Player A is better than Player C." Pure mathematical heresy! Transitive relations work beautifully in formal logic, but fall apart spectacularly when applied to sports matchups. No wonder LeBron's having an existential crisis—he's just discovered that his "greater than" comparisons between NBA legends violate the fundamental axioms of set theory. Next time someone tries to use the "A beat B beat C" argument, just whisper "non-transitive relations" and walk away like the math genius you are.

Using set theory to prove 1+1=2 is like bringing a nuclear submarine to a fishing trip. Sure, you've established that water is wet with the full might of mathematical formalism, but that smug expression says it all. Mathematicians spend years developing the foundations of arithmetic just to confirm what kindergarteners already know. Meanwhile, the rest of us are wondering if they'll ever use those big brains to figure out why the printer never works when you need it.

Mathematicians just collectively screamed! This meme pokes fun at the arcane debate between category theory and set theory as mathematical foundations. Category theory—with its abstract morphisms and functors—remains a niche field while set theory forms the backbone of math education. The joke suggests our technological progress has been stunted by this educational choice, implying that if we'd built math education on category theory's elegant abstractions instead, we'd have flying cars and futuristic cities by now. Meanwhile, most people are still trying to remember what a bijection is.

The mathematical nightmare that is Hilbert's Hotel strikes again! For the uninitiated, Hilbert's Hotel is a thought experiment with infinite rooms that are all occupied, yet can still accommodate new guests by having everyone move to the next room number. The infinite hotel manager's eternal struggle: "I am once again asking everyone to change rooms." Pure mathematical chaos wrapped in a Bernie meme format. Even with infinite rooms, the paperwork must be unbearable.

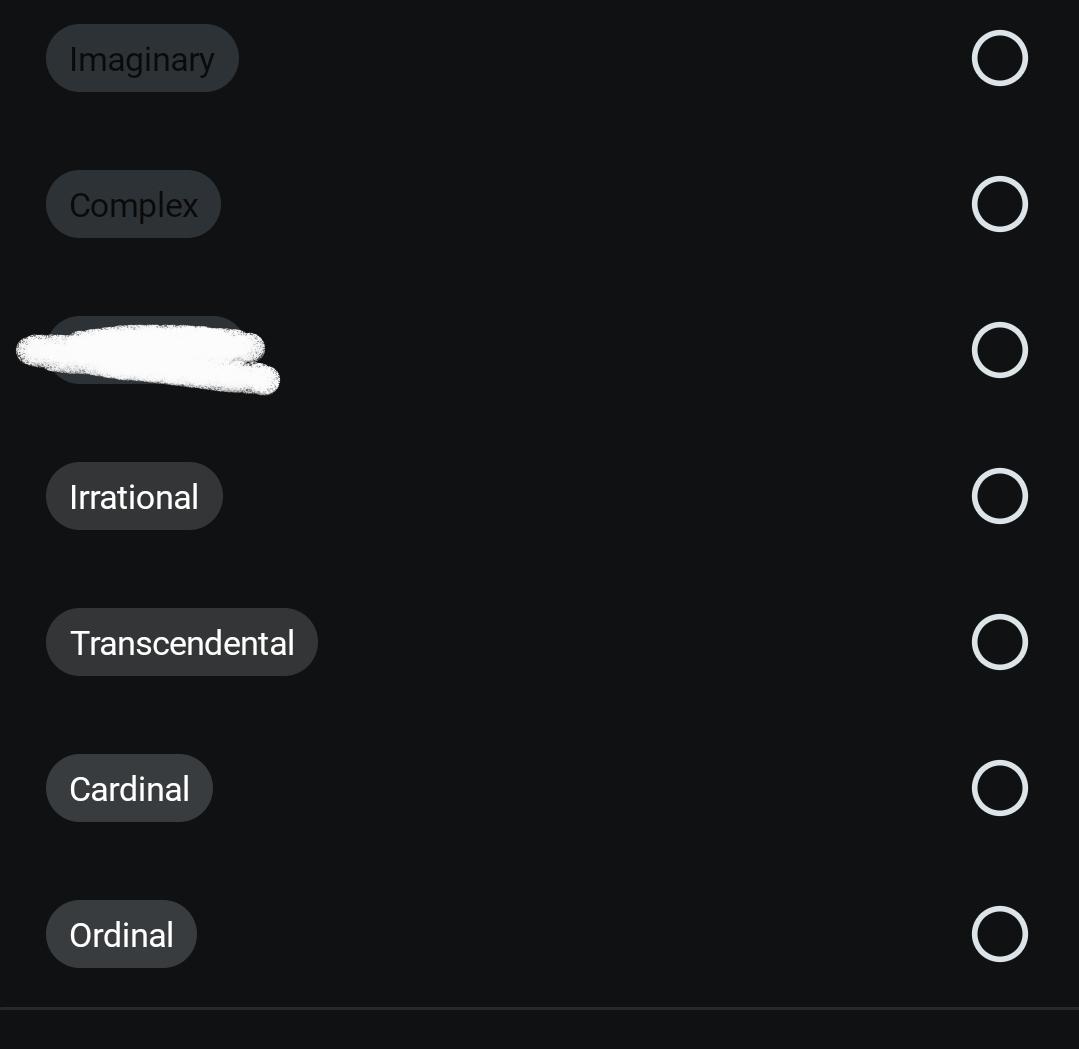
The meme shows a list of mathematical number types as checkboxes: Imaginary, Complex, [redacted], Irrational, Transcendental, Cardinal, and Ordinal. It's basically a mathematician's dating profile preferences! Instead of "seeking someone who loves hiking and cooking," they're filtering for numbers with specific properties. The joke works on multiple levels since many of these number types have relationships - like how all imaginary numbers are complex, and transcendental numbers are also irrational. Dating in the math world is just as complicated as the numbers themselves!

The Japanese flag just got a topology upgrade. That mathematical statement translates to "Japan is an open set" - meaning for any point in Japan, there's some tiny neighborhood around it that's still in Japan. The dashed boundary on the red circle is the mathematician's way of saying "we don't include the border" - just like how mathematicians insist on making simple concepts incomprehensible to normal humans. Next semester: proving why sushi rolls are topologically equivalent to donuts.

The divine existential crisis is real! This philosophical romp takes set theory to cosmic heights by applying Cantor's hierarchy of infinities to theological concepts. Just as ℵ₀ (aleph null) represents the first level of infinity in mathematics, our "god" character realizes he's just one deity in an infinite hierarchy of higher powers. The punchline hits when our creator—after contemplating his place in this infinite god-stack—decides the metaphysical recursion is too much and returns to his day job of cosmic mischief. It's basically what happens when you give omnipotent beings access to advanced mathematics and an edible.

The divine existential crisis hits different when you introduce transfinite numbers! This meme brilliantly combines theology with Cantor's set theory, where ℵ₀ (aleph null) represents the cardinality of natural numbers—the smallest infinity. The "god" character realizes that if infinite hierarchies exist (like how ℵ₁ > ℵ₀), then maybe there's a "god+1" above him. The recursive "turtles all the way up" reference is peak mathematical humor—basically the deity version of imposter syndrome. Poor guy just wanted to cause some suffering, but got sidetracked by ordinal arithmetic!

The joke here is a brilliant mathematical pun! When someone mentions a "new branch of maths" but it's actually just set theory, it's like saying "I discovered something revolutionary!" when it's actually one of the fundamental frameworks of mathematics. It's equivalent to a chef announcing they've invented a groundbreaking culinary technique called "heating food." The cat's wide-eyed expression perfectly captures the reaction of every math enthusiast who realizes they've been bamboozled by mathematical clickbait. Set theory is literally the foundation that modern mathematics is built upon—it's like claiming you've discovered a new continent called "Earth."

Programming nerds having existential crises over set theory is peak academia. Left guy says {{1}, {}} (empty set with element 1), middle guy is screaming about syntax errors, and right guy offers {{1}, 2} (set containing 1 and 2). The question asks for the complement of 2 in {{1}, 2, {}}. The answer? Depends if you're a computer scientist or mathematician! In set theory, the complement would be {{1}, {}} (everything except 2). But in programming, you might get that syntax error because 2 isn't a set. This is why mathematicians and programmers can't share an office without bloodshed.

The entire structure of mathematics precariously balanced on a few wooden poles labeled "ZFC." That's literally how it works, folks. Mathematicians built this elaborate skyscraper of theorems and proofs, and the whole thing rests on Zermelo-Fraenkel with Choice—a set of axioms we just... decided to accept. It's like watching a trillion-dollar mansion supported by IKEA furniture. The Axiom of Choice is particularly sketchy—it basically says "trust me bro, you can make infinitely many choices at once." And yet without it, half of modern math collapses faster than that building. Next time someone tells you math is the language of absolute truth, show them this architectural masterpiece.

The punchline here is "bijection" - a fundamental concept in mathematics where each element of one set is paired with exactly one element of another set. It's the mathematical equivalent of a perfect match! The meme creator cleverly disguised this nerdy math term as something that sounds like a risqué word. This is peak mathematical wordplay that would make Euler snort coffee through his nose. Only in the world of math could someone turn formal set theory into something that sounds like it belongs behind a convenience store counter.