Guys, I Did It: My Proof That P = Np. Fingers Crossed For The Fields Medal

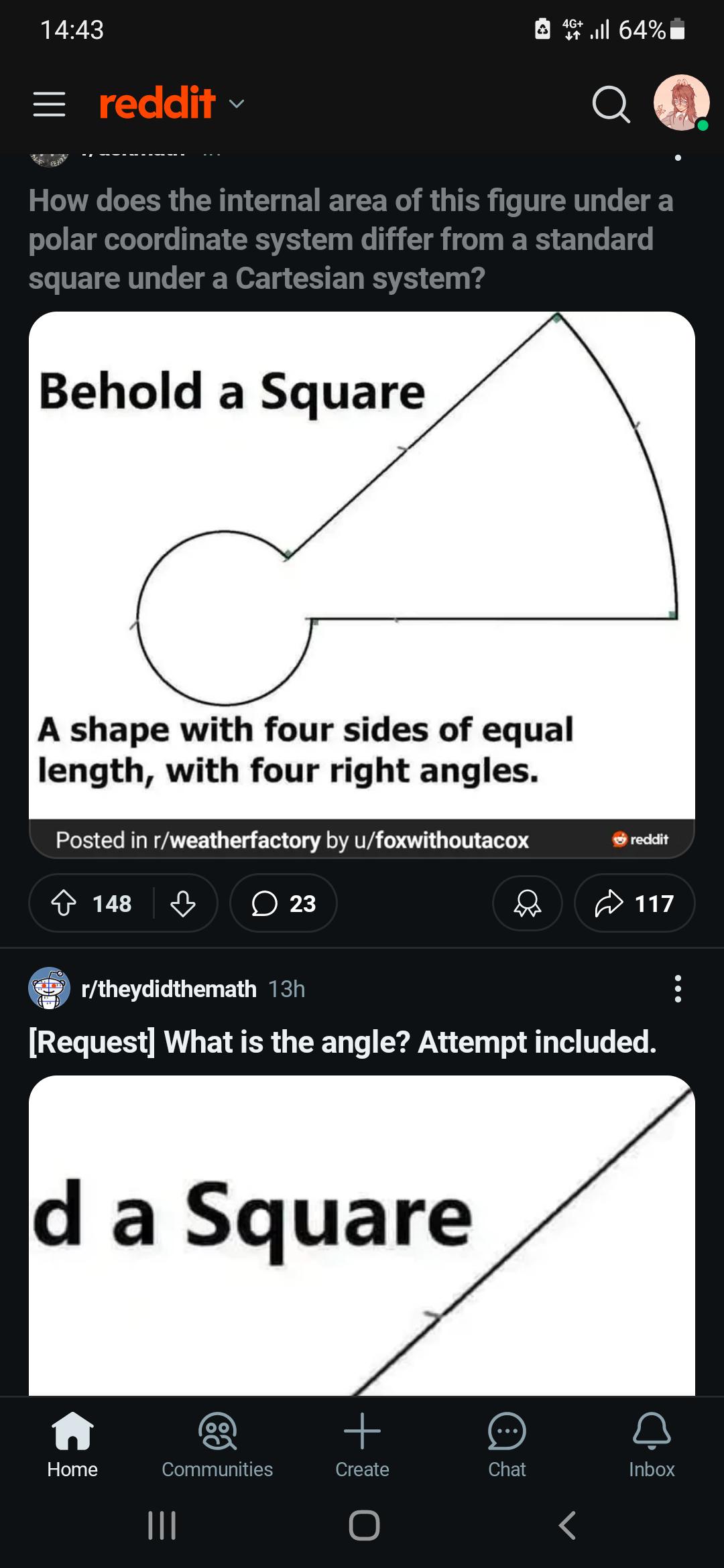
Content

A Simple Resolution of P = NP u/SlipPuzzieheaded7009 HUsuracu We present the first polynomial time algorithm for all problems in N, thereby proving of Cook and oano and Kart and gang 2. our method extends Valiant and gang's algebraic enumeration techniques 3 and 7 (1014 introduction The P vs NP problem- in Cook's 1971 theorem-provino work 1 and Karo's 1972 compilations of IF-complete problems 2 asks whether every problem whose solution can be verified in (n" time can also be solved in O(n) time We prove P = NP by devising a polv time solver that swn thesises circuit constructions a la vallant and gang.3 with certicate guided branching methods (Papadimitriou and gang 4). Our proof is rigorous and breathtakinglv concise mv wite's bovtriend told me so 5) Preliminaries All prior efforts are trivial and naive. Cook-Levin's reduction I is fine: SAI solvers are cute party tricks: POP theorems 6 are delightful and humorous. None saw the obvious that we have. Vain 'Theorem P= NP Proof Left as an exercise for the reader Results and Discussion SAT. CLIOUE. and Hamiltonian Cycle solved in O(n?) time Acknowledgments Tacknowledse. on bebslf of the entire mathematies community. the unparglleled senius of ruself Reterences . A. "The Complexitv of Theorem-Proving Procedures." STOC '71. ACM. 1971 2. Karp. R. M. "Reducibility Among Combinatorial Problems." in Complexity of Computer Valiant, L. G. "The Complexity of Enumeration and Reliability Problems." SIAM J. Comput. vol. 8. no. 3, pp. 410-421. 1979. :contentReference oaicite:2 index=2 4. Papadimitrion. C. H.. et al. *On the Complexity of Local Search in Combinatorial Optimize 6. Arora. S.. Safra. S. Probabilistic Checking of Proofs: A New Characterization of NP"