Unsolved problems Memes

From "I'm interested in the Collatz conjecture" to emailing a UCLA math professor claiming you've solved it after ChatGPT inflated your ego? That's not a proof, that's a mathematical tragedy in four acts! The Collatz conjecture has stumped brilliant minds for 85+ years, but sure, you "see the pattern" without advanced math. Next you'll be explaining how you've unified quantum mechanics and general relativity while waiting for your coffee to brew. Pro tip: If your mathematical breakthrough involves a rainbow clown wig, perhaps reconsider your life choices.

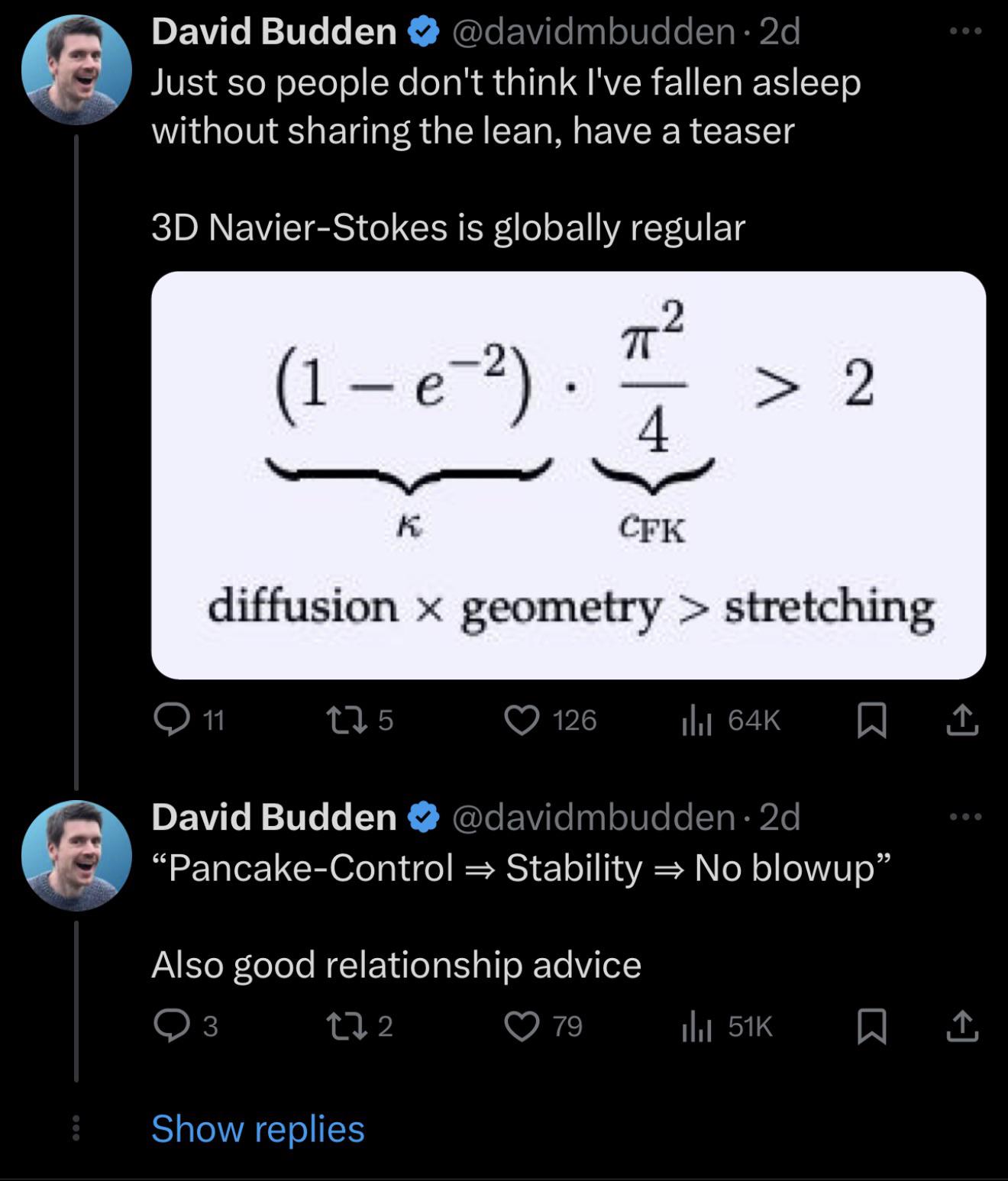
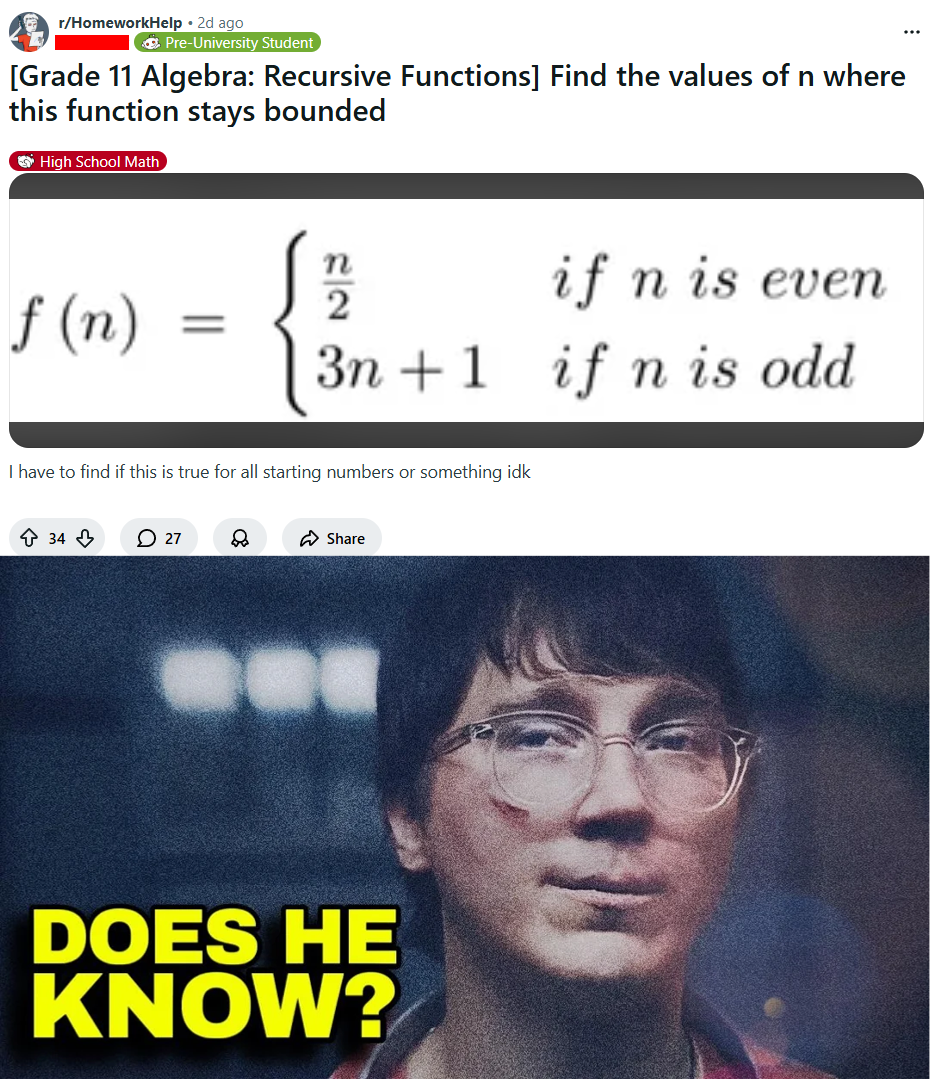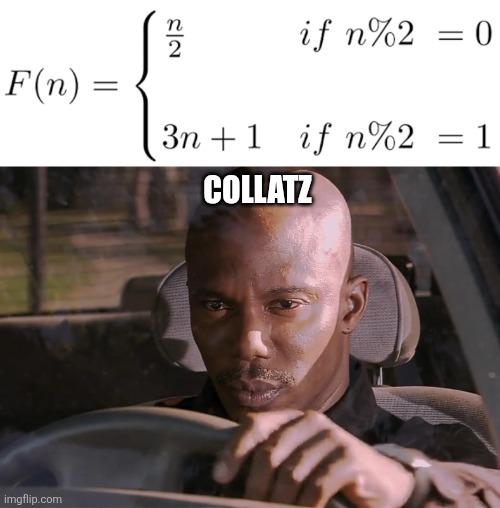This mathematical masterpiece shows Ed Sheeran's album progression (+, ×, ÷, =) followed by what could only be his most ambitious work yet: finding the zeros of the Riemann Zeta function! For the uninitiated, this infamous mathematical problem has stumped brilliant minds for over 160 years. The function ζ(s) = Σ(1/n^s) looks innocent enough, but proving all non-trivial zeros lie on a specific line (the Riemann Hypothesis) would literally earn you $1 million from the Clay Mathematics Institute. Imagine Ed dropping an album that casually solves one of the greatest unsolved problems in mathematics! His streaming numbers would be prime... I mean, prime-time amazing!

The mathematical equivalent of seeing Jesus in your toast! This guy's claiming to have solved the Navier-Stokes equations—one of math's million-dollar Millennium Prize Problems—while casually tweeting about it like he's sharing a breakfast recipe. The Navier-Stokes smoothness problem has stumped mathematicians for decades, but apparently all it needed was some "pancake control" and relationship advice. Next up: solving quantum gravity with a TikTok dance! What makes this extra hilarious is the perfect blend of genuine mathematical notation with completely unhinged conclusions. It's the academic equivalent of that 3AM eureka moment when you think you've discovered time travel but actually just need a sandwich and sleep.

The ultimate academic flex! George Dantzig walked into class late, saw two problems on the board, and thought "hmm, tough homework" - then casually solved two famous unsolved statistics problems that had stumped mathematicians for years. His professor must've been like "thanks for... breaking mathematics?" Talk about overachieving on an assignment that wasn't even an assignment! This is basically the mathematical equivalent of accidentally winning the Olympics while trying to catch a bus. The handshake meme perfectly captures that awkward moment when your professor realizes you've revolutionized statistics by mistake.

Poor kid just stumbled upon the infamous Collatz Conjecture disguised as homework. That function is a mathematical rabbit hole that's been driving professional mathematicians insane since 1937. Even with supercomputers, nobody can prove whether all starting values eventually reach 1. The "DOES HE KNOW?" caption is perfect—because no, he doesn't know he's facing one of math's most notorious unsolved problems while thinking it's just Grade 11 algebra. It's like accidentally wandering into a quantum physics exam when you signed up for basket weaving.

That moment when you're driving around with Goldbach's Conjecture living rent-free in your brain! Mathematicians have been suspecting since 1742 that every even integer greater than 2 can be written as the sum of two primes, but nobody's managed to actually prove it yet. It's like having the world's most annoying math riddle stuck in your head – you KNOW it's true (we've checked up to some ridiculously huge numbers), but try explaining that to your dissertation committee! The mathematical equivalent of "trust me bro" doesn't quite cut it in the proof department.

Mathematicians have been torturing themselves over Goldbach's Conjecture since 1742, and we're still not sure if it's true. The top panel shows the original statement: "All even numbers greater than 2 are the sum of two primes" which has resisted proof for nearly 300 years. The bottom panel shows the mathematically equivalent statement that's just worded differently: "All non-prime even numbers are the sum of two primes." It's like saying "I'll have a cheeseburger without pickles" versus "I'll have a pickle-free cheeseburger" and acting like you've revolutionized fast food. No wonder mathematicians can't get dates—they spend centuries arguing over semantically equivalent statements while the rest of us moved on after Euclid.

Ever innocently asked "Hey, can every even number greater than 2 be written as the sum of two primes?" and then realized you've just stumbled into Goldbach's Conjecture—a problem that's been tormenting mathematicians since 1742? That facepalm moment when your "simple curiosity" turns out to be one of mathematics' oldest unsolved problems. This is why I never ask questions in department meetings anymore. Next thing you know, you're dedicating your sabbatical to a problem that's been laughing at humanity for nearly 300 years.

The Collatz conjecture - that unsolved mathematical stalker that follows your every calculation! The formula shown is basically math's version of "I'll find you no matter what number you start with." For even numbers, divide by 2; for odd ones, multiply by 3 and add 1. No matter what positive integer you begin with, this function supposedly always leads back to 1 eventually, creating a numeric death spiral that mathematicians have been unable to prove for all numbers. It's like being in a mathematical horror movie where every path leads to the same inescapable end. Mathematicians have checked billions of numbers and still can't escape the Collatz curse!

The Collatz conjecture (3x+1 problem) is the mathematical equivalent of a horror movie for professional mathematicians. While students see it as a simple sequence where you multiply odd numbers by 3 and add 1, then divide even numbers by 2 until you reach 1, mathematicians are haunted by its unsolved status. Despite its innocent appearance, this problem has resisted proof for over 80 years, causing countless sleepless nights and broken chalkboards. It's basically math's version of "the call is coming from inside the house!"

That moment when you're introduced to the Twin Prime Conjecture and suddenly your entire weekend is gone. For the uninitiated, it's that unsolved math problem suggesting there are infinitely many pairs of primes that differ by 2 (like 3 and 5, 11 and 13). Mathematicians have been staring intensely at it since 1849 with exactly the same facial expression. Currently at "we know there are infinitely many primes that differ by at most 246" - which is like saying you're "almost" at the moon when you've reached the second floor.

Some mathematical theorems have been hanging around unsolved for decades, sometimes centuries. The P=NP problem is basically asking "are problems that are easy to verify also easy to solve?" Mathematicians have been staring at this since 1971, collecting million-dollar prize bounties, and still responding with the computational equivalent of a shrug. The rest of us are just standing here awkwardly, like that minion, waiting for someone to figure it out while the entire field collectively mumbles "no clue whatsoever." Maybe check back in another 50 years.