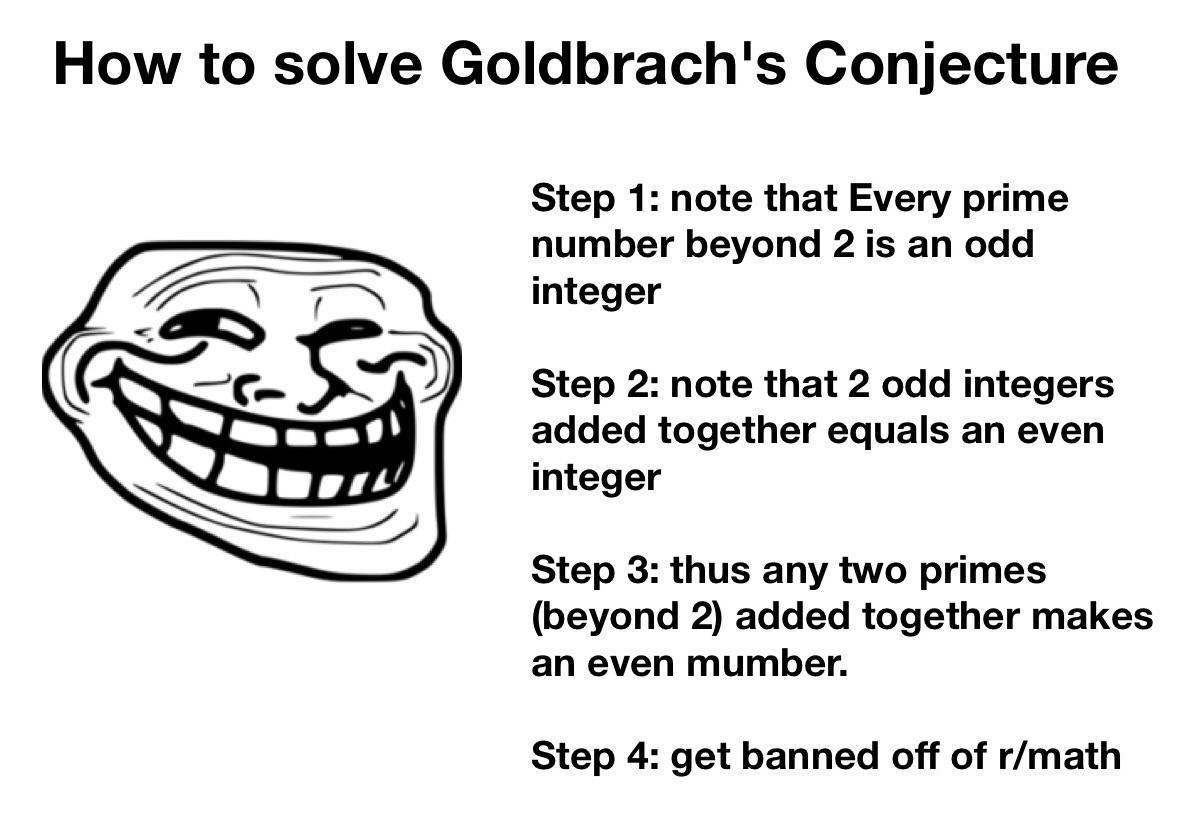
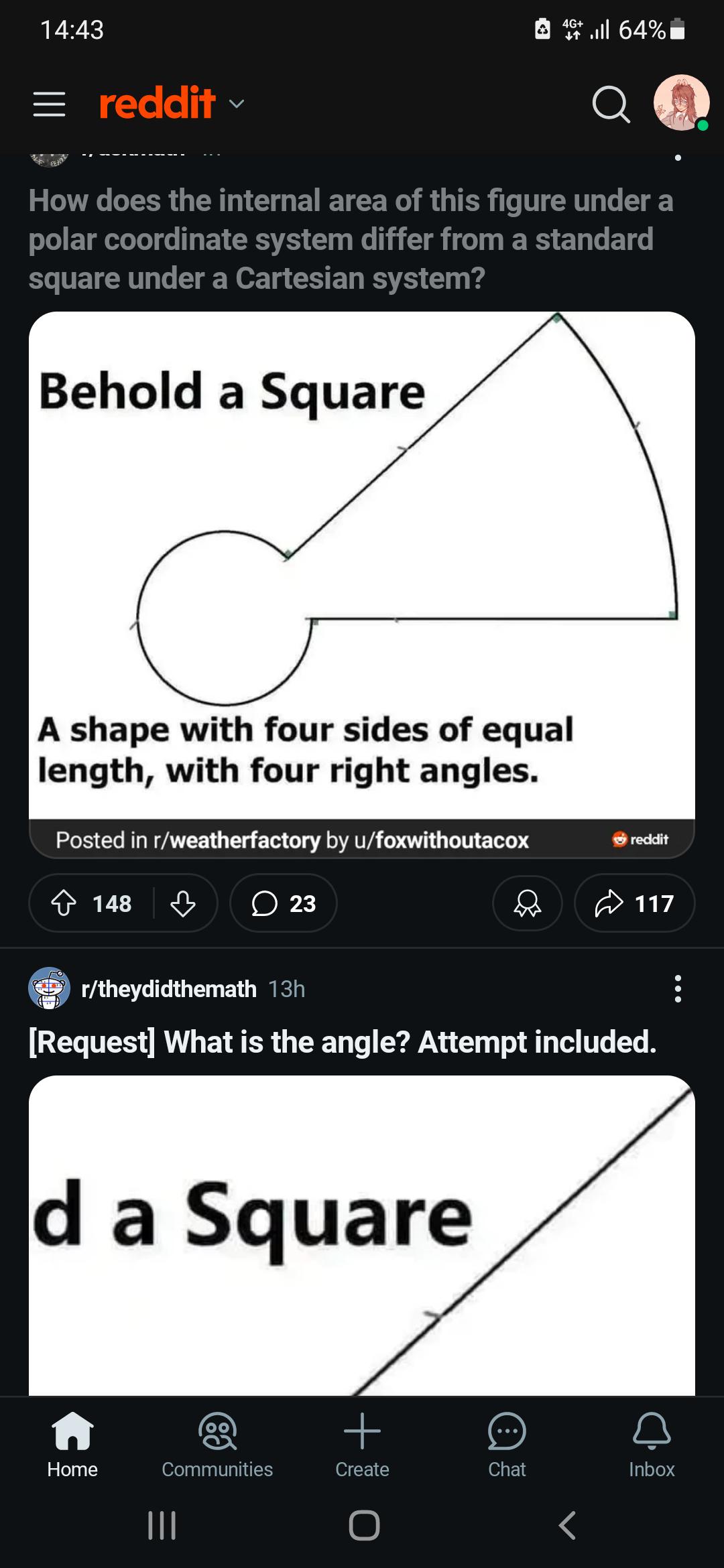
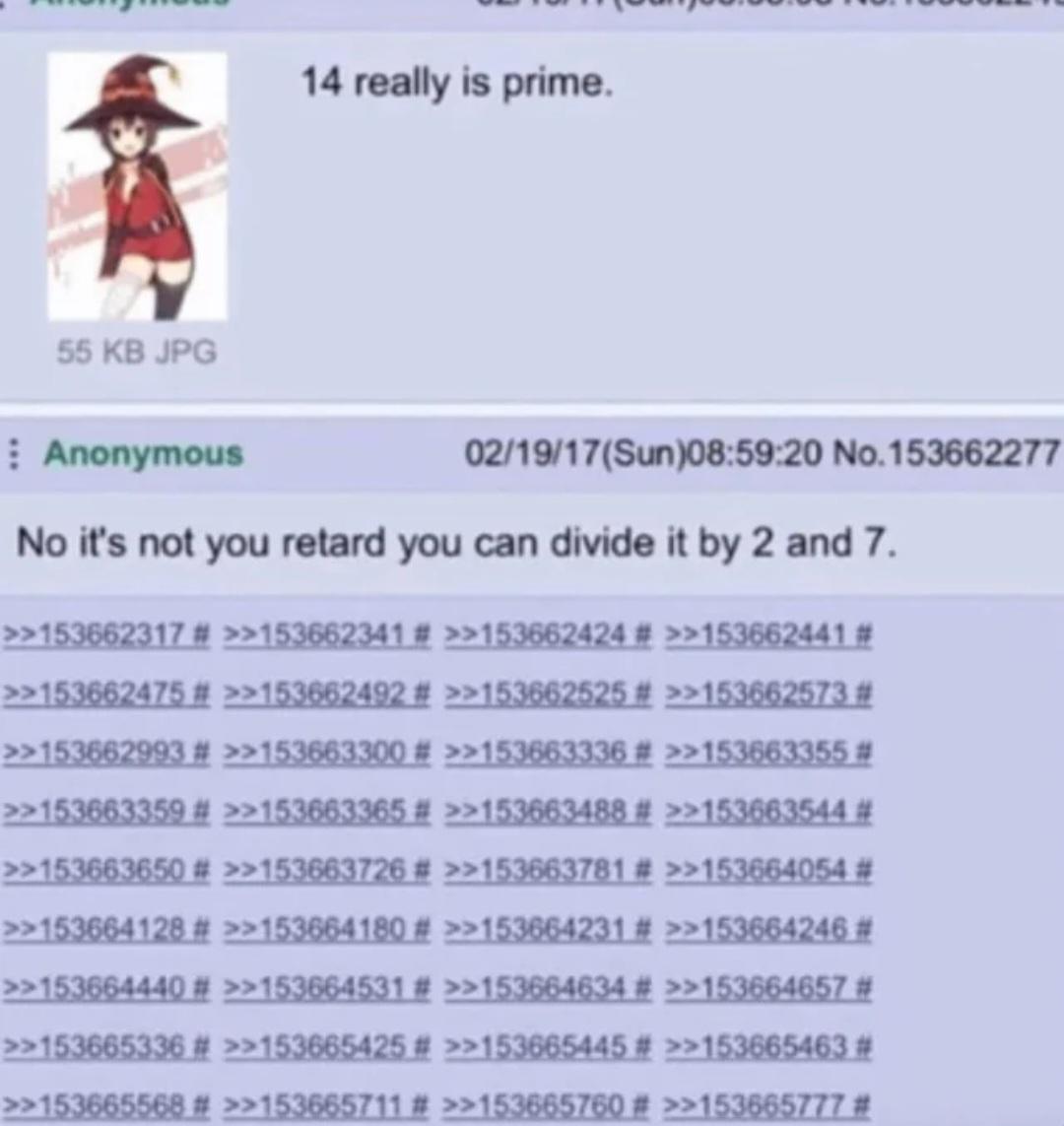
The equations look legit until you read them together. VP=nTR (ideal gas law), F=am (Newton's second law), c²m=E (mass-energy equivalence), and T⁻¹π2=ω (angular frequency)... but read the first letters down and you get "VFcT" which sounds like... well, you know. 🤦♀️ It's the scientific equivalent of rickrolling. Some physics student spent way too much time crafting equations that both work individually AND spell out profanity when read vertically. That's dedication to scientific trolling that deserves both a Nobel Prize and detention.


 Academia
Academia
 Ai
Ai
 Astronomy
Astronomy
 Biology
Biology
 Chemistry
Chemistry
 Climate
Climate
 Conspiracy
Conspiracy
 Earth-science
Earth-science
 Engineering
Engineering
 Evolution
Evolution
 Geology
Geology