Trolley problem Memes

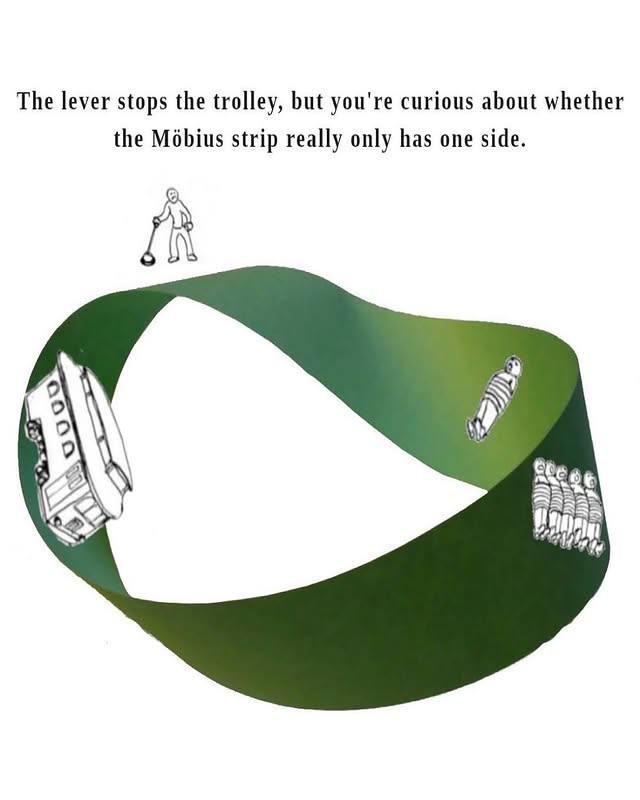
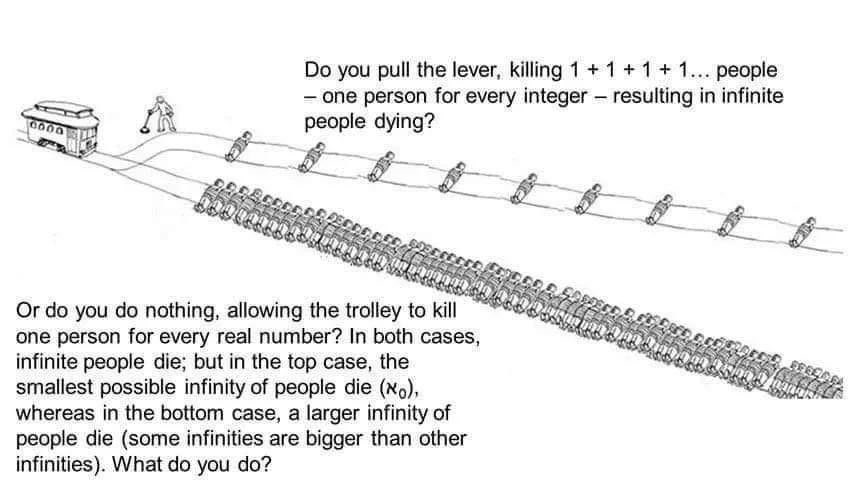
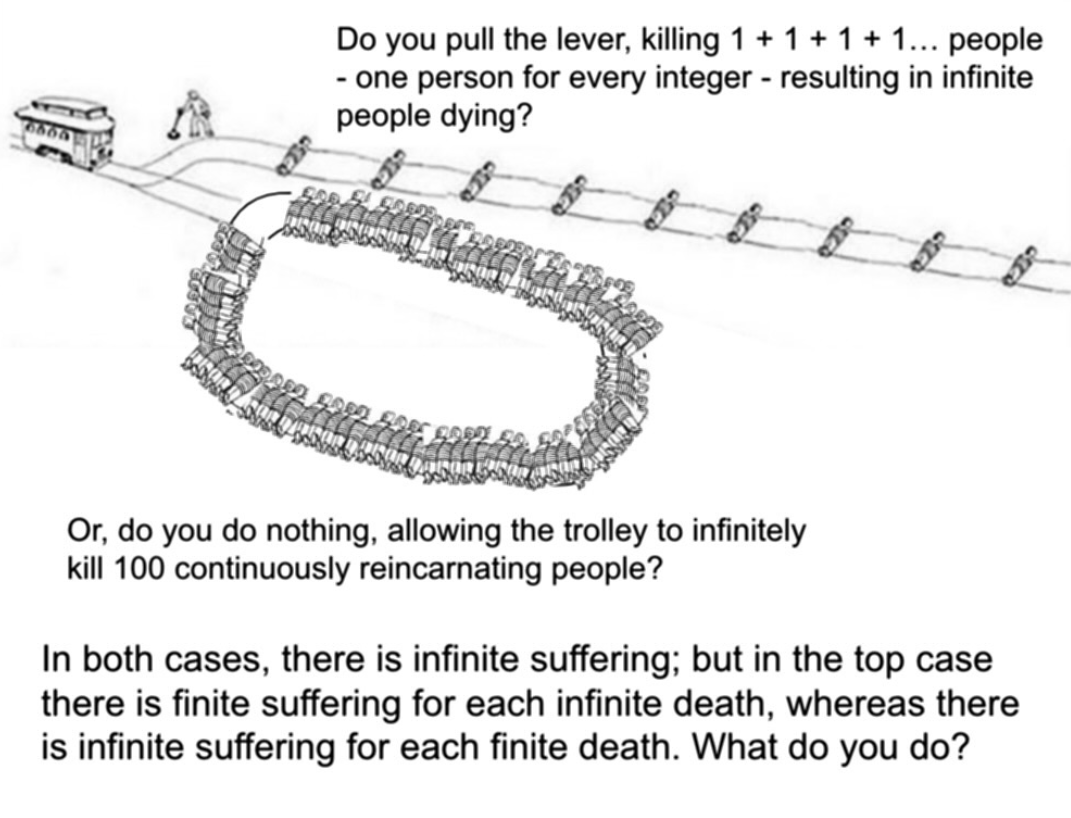
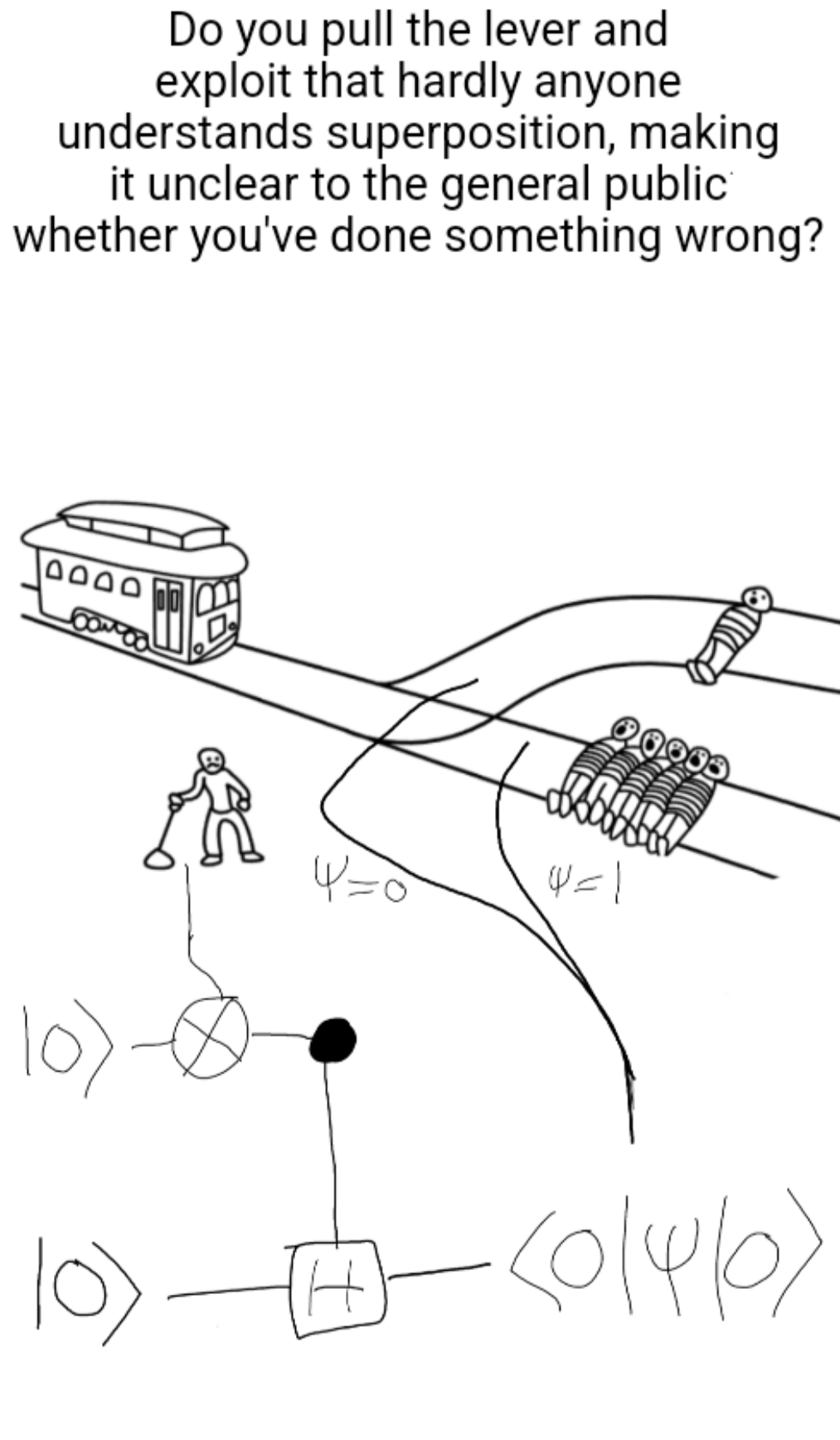
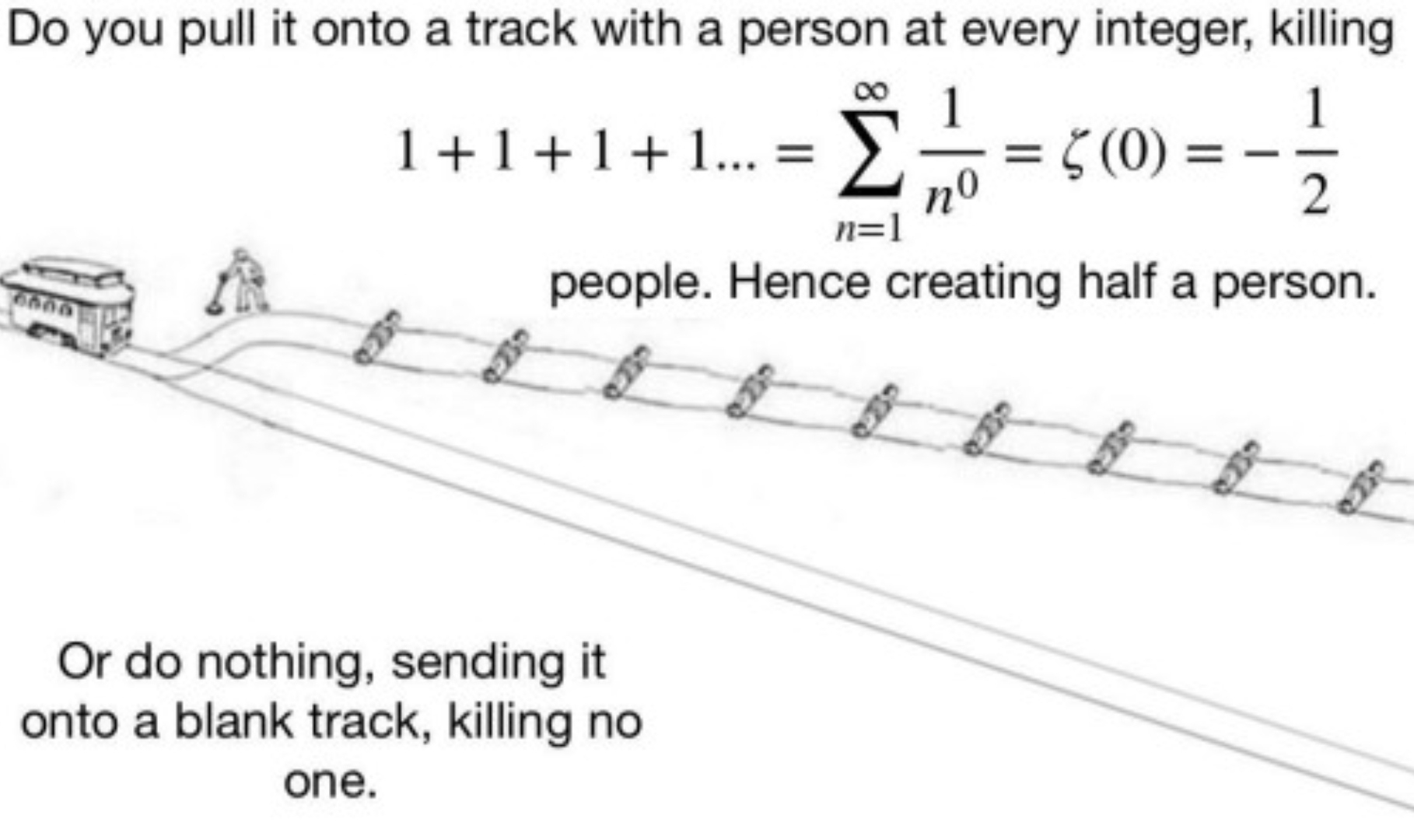
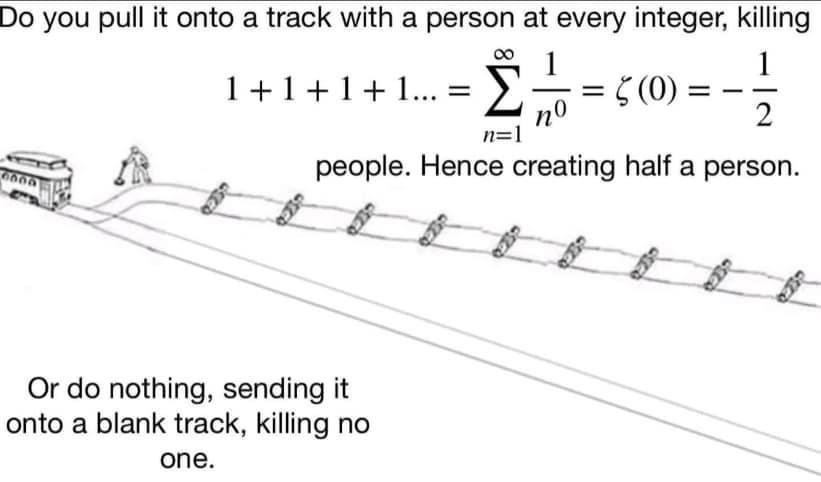
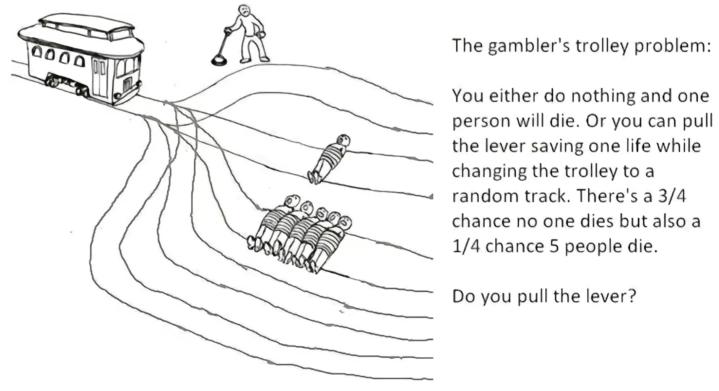
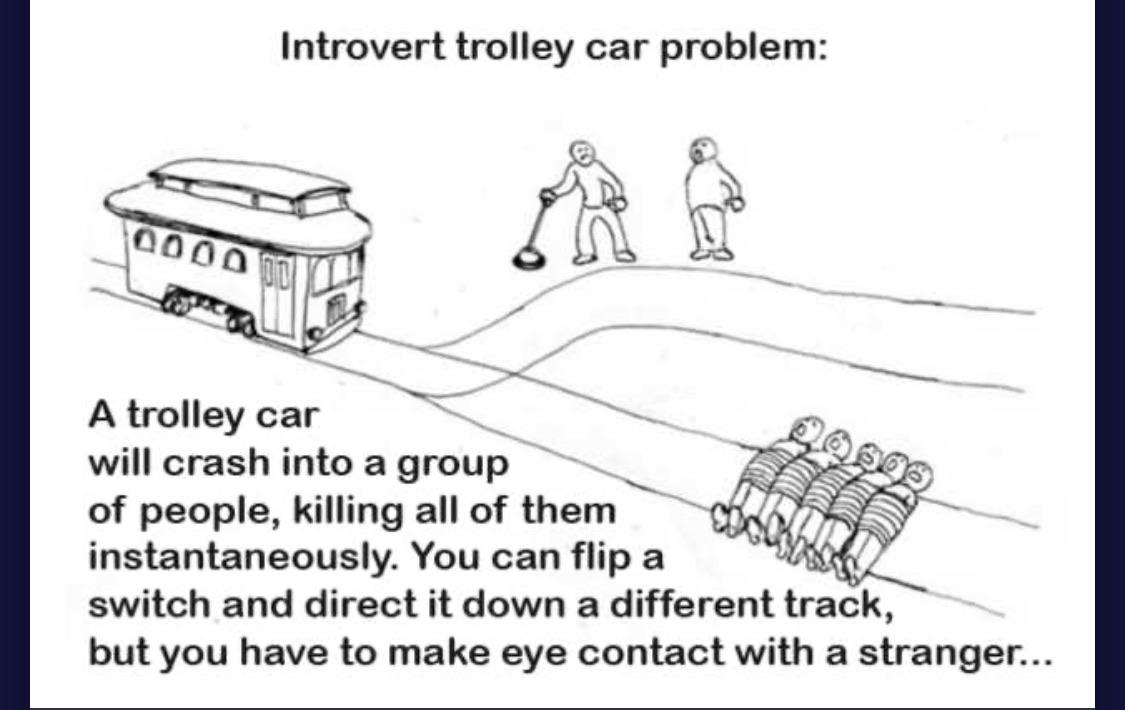
The ultimate mashup of quantum physics and moral philosophy! This meme brilliantly combines the famous double-slit experiment and Schrödinger's cat with the trolley problem in ethics. It's basically saying: "Here's a quantum version of the trolley problem where your measurement collapses the wave function and determines who lives or dies—oh, and by the way, you're philosophically ill-equipped to handle this because you're stuck in ancient virtue ethics." The quantum mechanics here is deliciously complex—wave-particle duality, entanglement, and measurement problems all wrapped into one ethical nightmare. In quantum mechanics, particles exist in superpositions until measured, at which point they "collapse" into definite states. Here, your measurement literally determines life and death across multiple possible universes! The final punchline about being a virtue ethicist who missed everything after Aristotle is the chef's kiss—imagine trying to apply Aristotelian ethics to quantum mechanics when you've missed 2,300 years of philosophical and scientific development. Talk about being underprepared for your physics final!