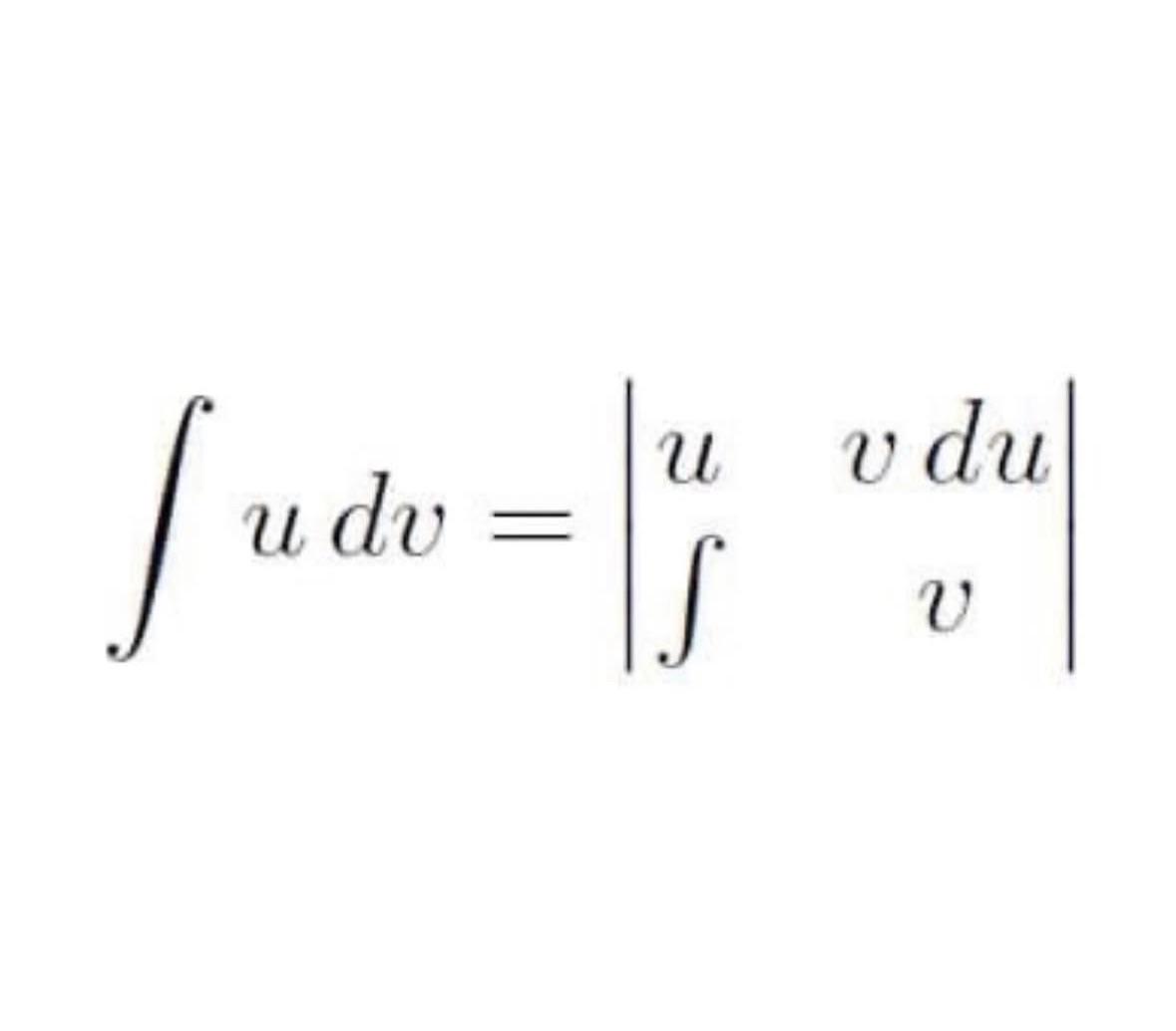Integration Memes

Who needs triple integrals when you've got an axe? While professors drone on about disk methods and shells, real calculus students are out here solving volume problems with pure brute force. "If I split this cube into enough tiny pieces, eventually one of them will give me the right answer!" Nothing says "I understand calculus" like turning a mathematical operation into a woodworking project. Next up: finding derivatives by aggressively drawing tangent lines with a chainsaw.

Mathematical mistakes as animal cruelty. That's a new one for the ethics committee. Someone's professor clearly got tired of students making common calculus errors. The logarithm product rule, inverse trigonometric functions, and basic integration - all weaponized with cute animals as collateral damage. Next time you write ln(a+b)=ln(a)+ln(b), just remember you're personally responsible for feline genocide. No pressure.

The calculus student's nightmare in mathematical form! This equation is missing the dreaded "dx" term needed to complete the integral. It's like showing up to the final exam and realizing you forgot your calculator, pants, and will to live. The equation itself is some physics monstrosity involving magnetic permeability (μ₀) and what appears to be a force calculation, but without that crucial "dx" differential element, it's mathematically incomplete. Just like my coffee mug that says "I differentiate, therefore I integrate... usually."

The first three integrals? Simple, elegant, textbook solutions. The fourth one? Pure mathematical chaos. That's the Gaussian integral for you—no elementary function can express it, just an infinite series that makes mathematicians wake up in cold sweats. It's like expecting to solve a simple equation and suddenly being asked to explain why your lab budget tripled last quarter. The face says it all: math was going so well until it wasn't.

The mathematical journey from simple to absolutely horrifying in four panels. First, our protagonist confidently handles a straightforward line equation with √(1+a²)x. "Yeah, that makes sense!" Second panel shows arcsin(x) with a semicircle graph. Still manageable. "Yeah, I can see that." Then panel three hits with the mathematical equivalent of a jump scare: x√(1+4x²)/2 + (1/4)ln(|√(1+4x²)+2x|). The character's expression says it all before we get to the final panel's existential crisis and profanity. Fun fact: This is actually showing different forms of calculating arc length for various functions, getting progressively more nightmarish. It's the calculus equivalent of starting with "hello" in a foreign language and suddenly being asked to negotiate international trade agreements.

The mathematical punchline that haunts calculus students everywhere! The top shows an integral of "ASPIRI dN" which equals... wait for it... Aspirin Plus C! Every calculus student knows the cardinal sin of integration is forgetting to add the constant of integration (+C). This meme brilliantly transforms that mathematical anxiety into pharmaceutical relief. The integration constant C isn't just a mathematical requirement—it's literally vitamin C in the medication! Next time your professor marks your homework wrong for forgetting +C, just tell them you're saving it for your headache later.

This is peak calculus humor right here! The integration by parts formula (∫udv = uv - ∫vdu) brilliantly represented with a UV light minus a voodoo doll. That moment when mathematical wordplay transcends into visual punnery is just *chef's kiss*. Anyone who's survived Calculus II knows the existential dread of applying this formula only to end up with an integral more complicated than what you started with. It's like the mathematical equivalent of trying to escape a labyrinth but digging yourself deeper with each turn. Pure mathematical masochism!

This meme perfectly captures the eternal mathematical debate: summation vs. integration! On the left, we have Sigma (Σ), represented by a stepped escalator with distinct, countable steps—just like how summation adds discrete values. On the right, the integral symbol (∫) is represented by a smooth escalator, showing the continuous nature of integration where we're calculating area under a curve. Every mathematician has a preference, but we all know which one is easier on exam day. Discrete steps or smooth sailing? Your calculus professor is judging your choice right now.

Integration by parts. The mathematical equivalent of being told "you're going to have to take the long way home." Just when you think you've simplified the problem, it hands you back something more complex than what you started with. The calculus version of a cruel practical joke that's been tormenting undergrads since 1684. Your professor says it's elegant. Your tear-stained homework says otherwise.

That moment when your calculus professor casually writes "integrate this" and walks away. The expression √u/du is the mathematical equivalent of being handed a broken screwdriver and told to build a spaceship! Integration by substitution? Parts? Sacrifice to the math gods? This is where students silently mouth "what dark magic is required here?" while frantically flipping through textbooks. The perfect representation of that collective math trauma we've all experienced!

The mathematical flex nobody asked for! This meme showcases the infamous Dirichlet function - the rebel of calculus that equals 1 for irrational numbers and 0 for rational ones. The poor function is literally screaming its values while mathematicians argue about its supremum and infimum (fancy terms for maximum and minimum values). And yet, despite having values of both 0 and 1, this function is so pathologically broken that it can't be integrated using standard methods. It's basically the mathematical equivalent of that friend who technically meets all the requirements for the party but still manages to ruin everyone's night. No wonder calculus professors use it to crush the souls of unsuspecting undergrads!

The integral of "aspiri dn" equals Aspirin Plus C! This brilliant calculus pun plays on the fact that when you integrate a function, you always add "+ C" (the constant of integration). So integrating "aspirin" gives you "Aspirin + C" — exactly what's shown on that medication box! Mathematical wordplay that would make your calculus professor both proud and slightly nauseated simultaneously.