Homeomorphism Memes

Topologists see the world differently than the rest of us. To them, a fidget spinner and a donut are mathematically identical - both have exactly one hole! In topology, it's all about properties that don't change when an object is stretched or bent (without tearing). So carrying a fidget spinner is basically carrying a portable donut... minus the calories and sugar rush. The perfect mathematical snack for your pocket!

The genius of this meme lies in topology's fundamental principle: a donut and a coffee mug are mathematically identical because they both have exactly one hole. Similarly, the first image shows jeans as a "single tube" (one hole for both legs), while the second shows two separate pant legs (two holes). To a topologist, these are fundamentally different objects! It's basically fashion advice from mathematical theory—where the number of holes is what truly matters.

The perfect collision of abstract math and real life! The top panel shows topological equivalence - where mathematicians consider a donut and a coffee mug to be identical shapes because they both have exactly one hole. In topology, it's not about appearance but the fundamental properties that remain unchanged during continuous deformation. Then reality strikes! The bottom panel shows someone trying to unlock a bike with a combination lock - suddenly topology becomes VERY relevant. Try explaining to your stolen bike that "technically" your lock was topologically sound! Turns out mathematicians' casual dismissal of practical geometry might not hold up when your transportation depends on it. Pure math meets street smarts in the most painful way possible!

The experiment was going smoothly until the coffee mug showed up! What we're witnessing is a topologist's nightmare - three perfect toruses (donuts) in a row and then BAM! A simple coffee mug crashes the topology party! In the wild world of topology, a coffee mug and a donut are actually the same shape (both have exactly one hole), but try telling that to the scientist monitoring this experiment! The stick figure's "all good so far" comment is about to age like milk left in a quantum physics lab over spring break. That mug is the mathematical equivalent of wearing socks with sandals to a fashion show!

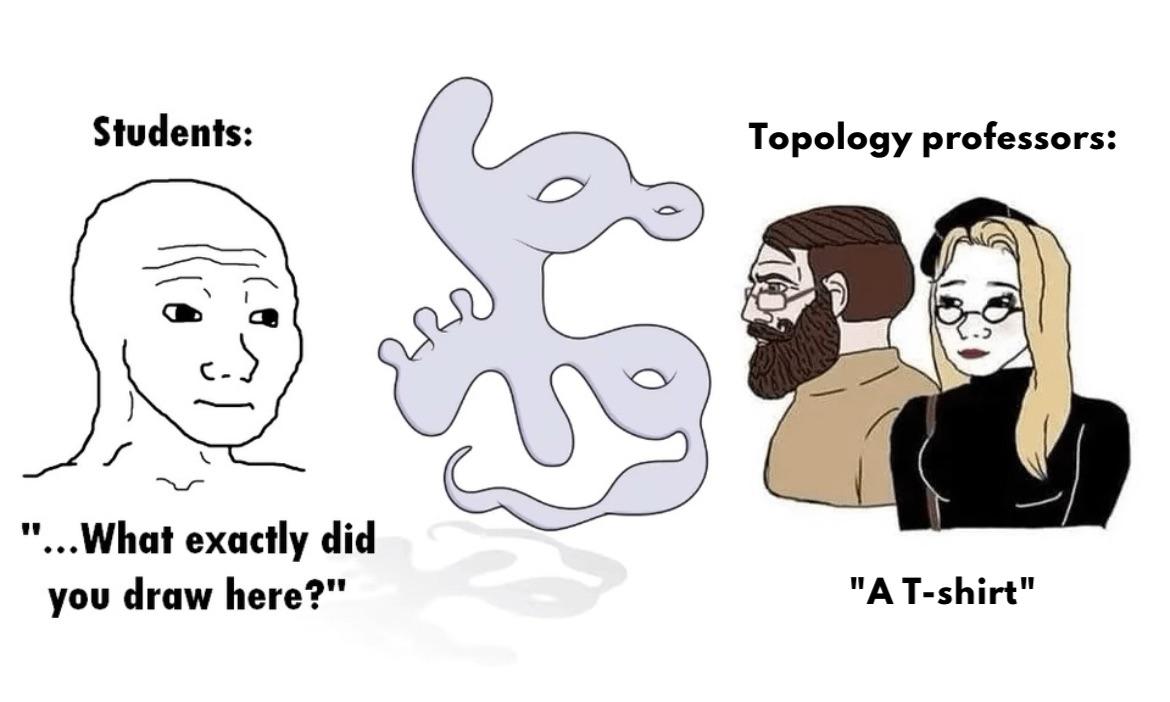
Welcome to the mind-bending world of topology, where a coffee mug is mathematically identical to a donut! In this meme, a confused student sees an abstract blob with holes and asks "What exactly did you draw here?" Meanwhile, the topology professors confidently declare it's "A T-shirt." This is peak topology humor because in this field, objects are defined by their fundamental properties (like number of holes) rather than their exact shape. To a topologist, that weird blob could indeed be a T-shirt since they both have the same number of holes (three - one for the torso, two for the arms). The actual appearance is irrelevant! Next time someone questions your drawing skills, just claim you're working in "topological space" and walk away smugly.

Mathematical functions having an identity crisis! The meme pokes fun at homeomorphism in topology, where functions need specific properties to qualify. The first function proudly declares "I'm bijective" (maps every element uniquely), another claims "I'm continuous" (no sudden jumps), but the third screams "I'M NOT!" - ruining their chances at being a homeomorphism. For a valid homeomorphism, both the function AND its inverse must be continuous. That forgotten check is the mathematical equivalent of showing up to a fancy party missing your pants. Classic mathematician humor where the punchline is literally a function that failed to check all its properties!

Ever seen a mathematician get excited over breakfast? This is why! In topology, a coffee mug and a donut are mathematically identical—both have exactly one hole, making them homeomorphic objects. The blue ceramic transformation perfectly illustrates how you can smoothly deform one into the other without tearing or gluing. Next time someone asks if you want coffee or a donut, just say "topologically speaking, I'll have the same thing either way" and watch their brain short-circuit. The real question isn't what you're having for breakfast—it's how many holes it has!

Finally, proof that topology isn't just theoretical nonsense! Here's a donut that's been transformed into a coffee mug, exactly as the mathematicians prophesied. The legendary "donut-to-coffee mug homeomorphism" has escaped the chalkboard and infiltrated retail stores! Next time your calculus professor goes on about continuous deformations, just show them this £6 masterpiece. It's like the universe is trolling mathematicians by making their abstract examples commercially available.

Welcome to Topology 101, where your kitchen utensils trigger existential crises! The bowl paradox is basically the philosophical equivalent of asking whether the glass is half empty or half full—except way more pretentious. Mathematicians would call this a homeomorphic transformation problem. To them, a coffee mug and a donut are literally the same object. I've spent 30 years teaching differential geometry, and students still look at me like I've lost my mind when I say that. Next week's assignment: determine if your pasta strainer is just a bowl with an identity crisis. Bring your existential dread and a #2 pencil.

To a topologist, a coffee mug and a donut are identical—they both have exactly one hole. This meme takes that concept to your wardrobe! The coffee cup is a simple torus, the shirt has three holes (one big one and two arm holes), and the socks are just spheres (zero holes). But those pants? That's where the joke gets its punch. Those aren't regular pants—they're "blue jeans with belt loops," meaning they're topologically distinct with multiple holes. In topology, it's not shape that matters but the number of holes. Your fashion sense might be questionable, but your topological classification is impeccable!

To a topologist, a coffee mug and a donut are identical because they both have exactly one hole. Similarly, letters like A, B, C, D, P, and R are all topologically equivalent—they each have a single hole! The frustrated character is typing what looks like gibberish to us, but to a topologist, they're just repeating the same letter over and over in different fonts. Why use different symbols when they're fundamentally the same shape? Mathematical efficiency at its finest!

Topologists staring at this meme like it's their job interview. To them, a coffee mug and a donut are literally identical objects—both have exactly one hole. This is the mathematical equivalent of saying "potato, potato" except it's "caffeine delivery system, breakfast pastry." Corporate might want differences, but in topology, it's all about counting holes and ignoring everything else. Just wait until they learn about Klein bottles...