Holes Memes

The topology kid isn't wrong! In topological terms, digging a hole in the ground doesn't actually create a "hole" - it's just a depression that's topologically equivalent to the original surface. A true topological hole would require puncturing all the way through the Earth! The parent thinks they're just digging a simple pit, but their mathematically precocious offspring recognizes this isn't creating a new genus in the surface. Topologists see the world differently - to them, a coffee mug and a donut are identical because they both have exactly one hole. Your kid's not being rude; they're just preparing for a future where they'll correct their calculus professor.

The genius of this meme lies in topology's fundamental principle: a donut and a coffee mug are mathematically identical because they both have exactly one hole. Similarly, the first image shows jeans as a "single tube" (one hole for both legs), while the second shows two separate pant legs (two holes). To a topologist, these are fundamentally different objects! It's basically fashion advice from mathematical theory—where the number of holes is what truly matters.

The great topology debate that's splitting friendships and ruining dinner parties everywhere! 🤣 In topology (the mathematical study of shapes and spaces), a straw is actually a cylinder with a single continuous hole running through it - making it topologically equivalent to a donut or coffee mug! The diagram hilariously tries to "flatten" the straw into a disk with a hole, but our cereal-eating friend is having NONE of that mathematical trickery. This is basically the mathematical version of "is a hot dog a sandwich?" and I'm here for the chaos it creates! Mathematicians would side with "one hole" while the practical breakfast enthusiast counts the openings. Both technically right in different contexts - which is why it's such a perfect meme to start arguments with your smartest friends!

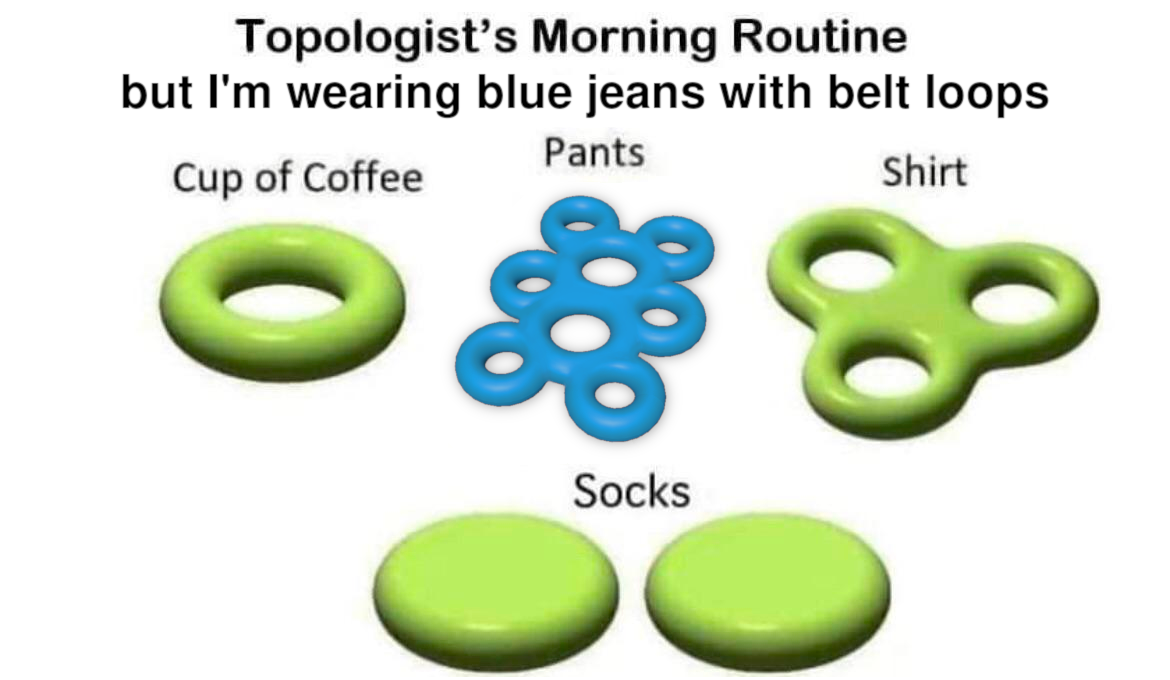
To a topologist, a coffee mug and a donut are identical—they both have exactly one hole. This meme takes that concept to your wardrobe! The coffee cup is a simple torus, the shirt has three holes (one big one and two arm holes), and the socks are just spheres (zero holes). But those pants? That's where the joke gets its punch. Those aren't regular pants—they're "blue jeans with belt loops," meaning they're topologically distinct with multiple holes. In topology, it's not shape that matters but the number of holes. Your fashion sense might be questionable, but your topological classification is impeccable!

This is what happens when math nerds get artistic! In topology, a donut and a coffee mug are actually the same shape (they both have exactly ONE hole). But this sculpture is having an existential crisis with its multiple holes! Topologists are obsessed with counting holes - it's literally their whole job. They study shapes based on properties that don't change when you stretch or bend them (without tearing or gluing). So to a topologist, this metal masterpiece isn't just pretty - it's a mathematical playground! The sculptor probably thought they were making art, but accidentally created a topology professor's dream exam question. "Count the holes and explain why this shape is homeomorphic to a pretzel with anxiety."

Topologists are having a collective nervous breakdown right now. This shape is basically the mathematical equivalent of finding a glitch in the Matrix. "A hole in a hole in a hole" is like telling a topologist their shoelace is untied, then watching them question their entire existence. In topology, counting holes isn't just about visible openings—it's about whether you can continuously deform one shape into another without tearing or gluing. This twisted monstrosity looks like what happens when a donut tries to eat itself while falling into a black hole. The number of holes? Depends if you ask before or after the topologist's therapy session.

In topology, the number of holes in an object is what matters, not its exact shape. So to a topologist, a coffee mug is literally identical to a donut (both have one hole), and your belt-looped jeans are just a weird multi-holed structure! These mathematicians reduce everyday objects to their "genus" (fancy word for hole count) and couldn't care less about trivial details like "is this a shirt or a fidget spinner?" Fun fact: this is why mathematicians joke that they can't tell the difference between their coffee cup and their donut at breakfast. The holes are all that matter in their delightfully warped reality!

Topologists everywhere are having a collective meltdown right now! That's a soccer ball with a giant hole—basically a topological nightmare. In topology, objects are classified by their number of holes (genus), and this ball just went from genus 0 to genus 1. It's like someone took a donut and said "this is definitely a sphere." The mathematical betrayal is real! Next thing you know, someone will try convincing us that coffee mugs and donuts are different objects.

Ever wondered what mathematicians wear to parties? For topologists, a shirt with three holes and pants with two holes are mathematically identical! In topology, objects are classified by their "genus" (number of holes), not their shape or size. So that plaid "shirt" and blue "pants" are topologically equivalent structures—both with multiple holes. Fashion crisis solved! Next time someone complains about your outfit, just tell them it's topologically correct.

The philosophical topology paradox that keeps physicists up at night! From a mathematical perspective, a bowl is just a specific type of hole with extra steps. It's a genus-1 topological surface (same as a coffee mug) defined by what's not there. The negative space becomes the functional feature! Mind = blown. This is basically the geometric equivalent of realizing water isn't wet—water makes other things wet. Next time you eat cereal, remember you're pouring milk into an elaborate hole disguised as a kitchen utensil.

The topology enthusiast is having an existential meltdown because in mathematical topology, a "hole" isn't something physically dug but rather a fundamental property of space! In topology, surfaces are classified by their genus (number of holes), but these aren't actual excavations—they're abstract properties of connectedness. So technically, no hole has ever been "dug" because holes in topology exist as mathematical properties rather than physical voids. Meanwhile, the regular person is just talking about the Kola Superdeep Borehole without realizing they've triggered a mathematician's worst nightmare.

The eternal mathematical debate that keeps topologists awake at night! Is a watering can a 1-hole or 2-hole object? The handle creates one hole, but what about the spout? Does it connect to the main chamber making it all one hole? Or is the spout a separate hole entirely? *twirls chalk maniacally* This is why mathematicians can't garden—they spend hours debating the topology instead of watering the plants! Meanwhile, the plants have died of thirst while we're still counting holes. Genus calculations have never been so... moist! 💦