Cartography Memes

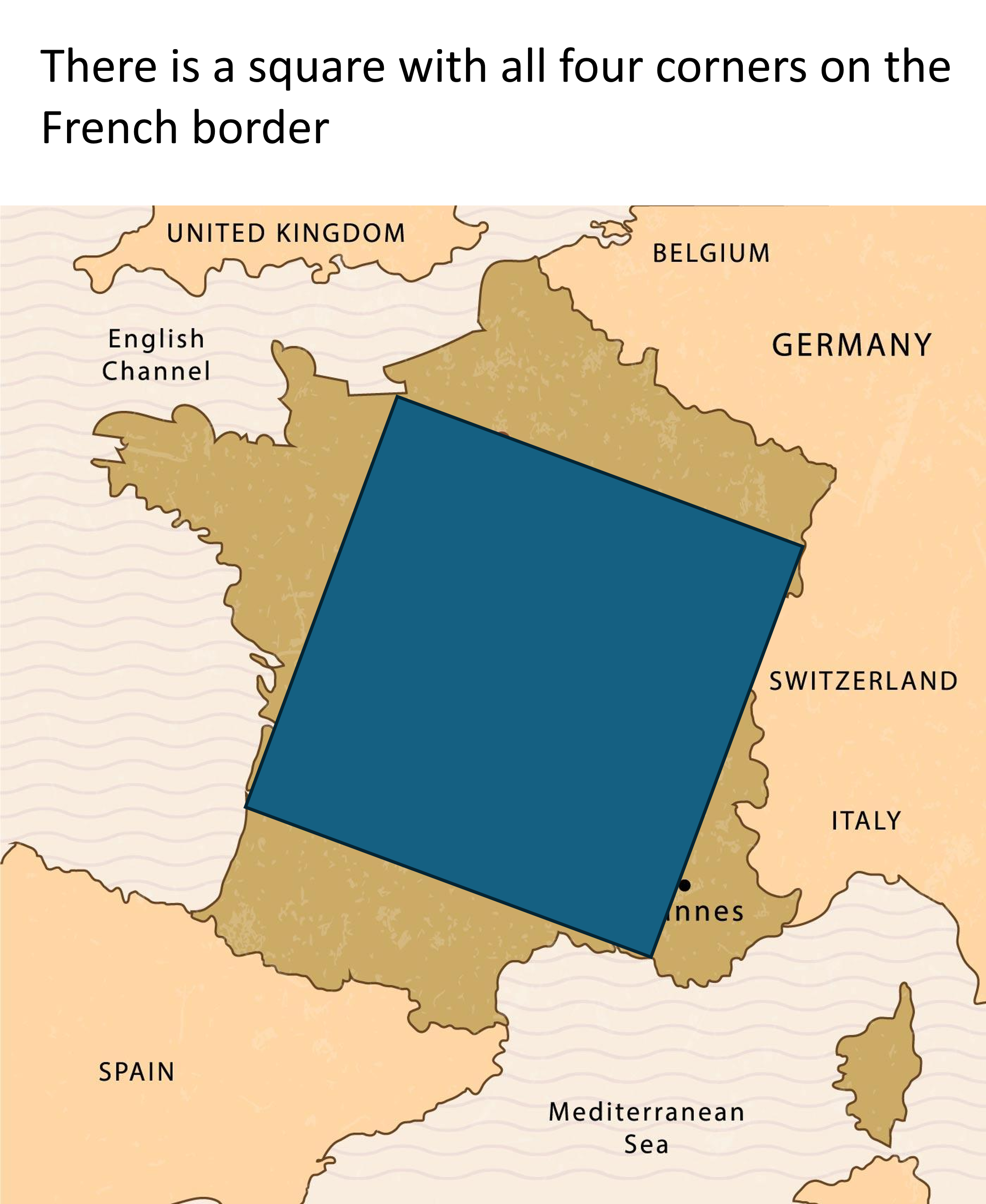
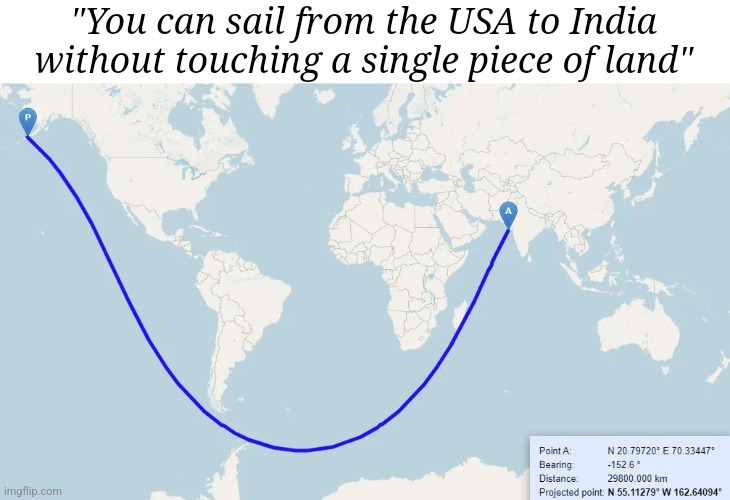
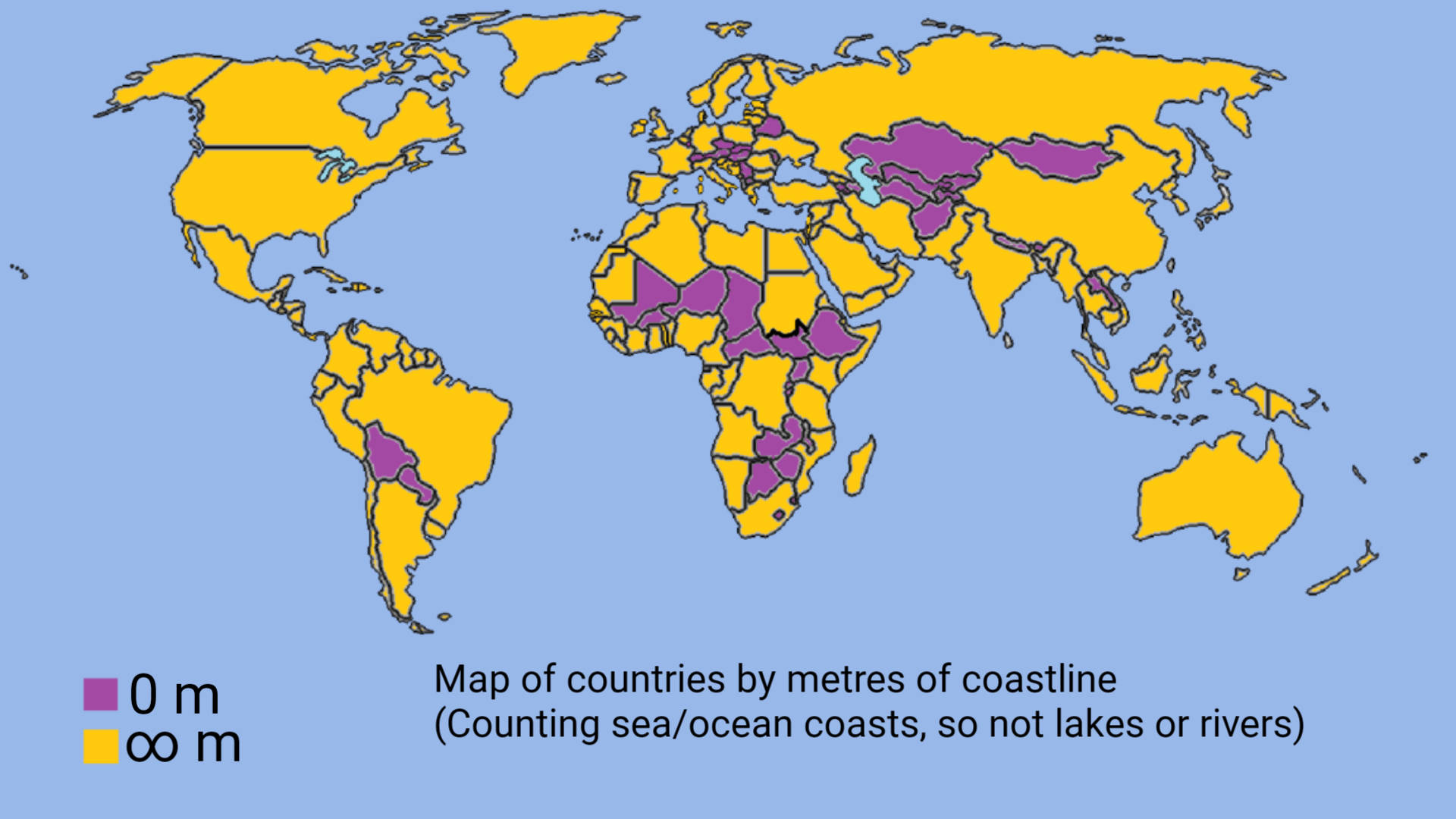
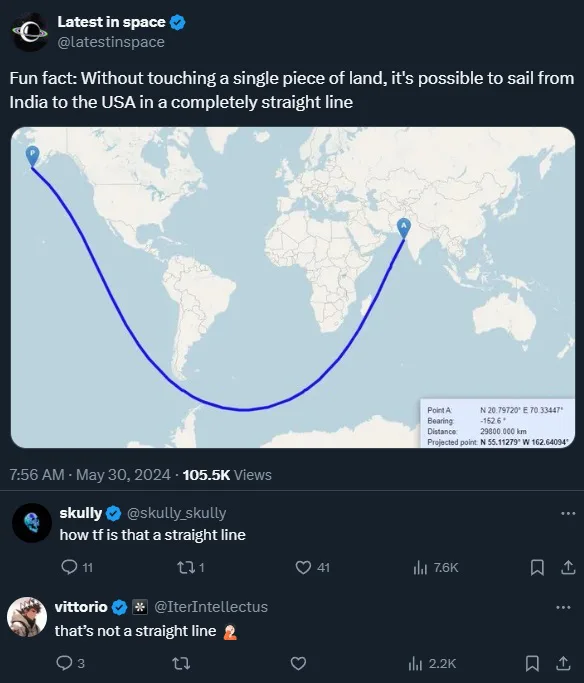
The perfect illustration of the Dunning-Kruger effect in cartography! That curved blue line represents the shortest path between two points on a globe (a geodesic), but mapping it onto a flat projection creates this apparent curve. The bell curve shows three perspectives: the confident-but-wrong crowd ("it's straight!"), the technically correct experts ("it's bent around Earth's curvature"), and my personal favorite—the person who just uses their eyeballs ("I can clearly see it's not straight"). What makes this extra hilarious is that the 20,000,000 km distance shown would actually be about 50 times Earth's circumference—so nobody's right! The ultimate cartographic mic drop for anyone who's ever argued about the "best" map projection.

The meme beautifully captures the collision between map projections and spatial reasoning! The original tweet claims you can sail from India to the USA in a "straight line" without touching land, showing a curved path on a flat map. But here's the mind-bender: that curved line is actually geodesically straight in 3D space! When sailing across a spherical Earth, the shortest path (a "straight line" in navigation terms) follows what's called a great circle. On flat Mercator projections, these great circles appear curved because... well, you're squishing a sphere onto a rectangle! The commenters missing this concept is pure comedy gold. It's like watching someone argue that the Earth is flat while standing on a globe!