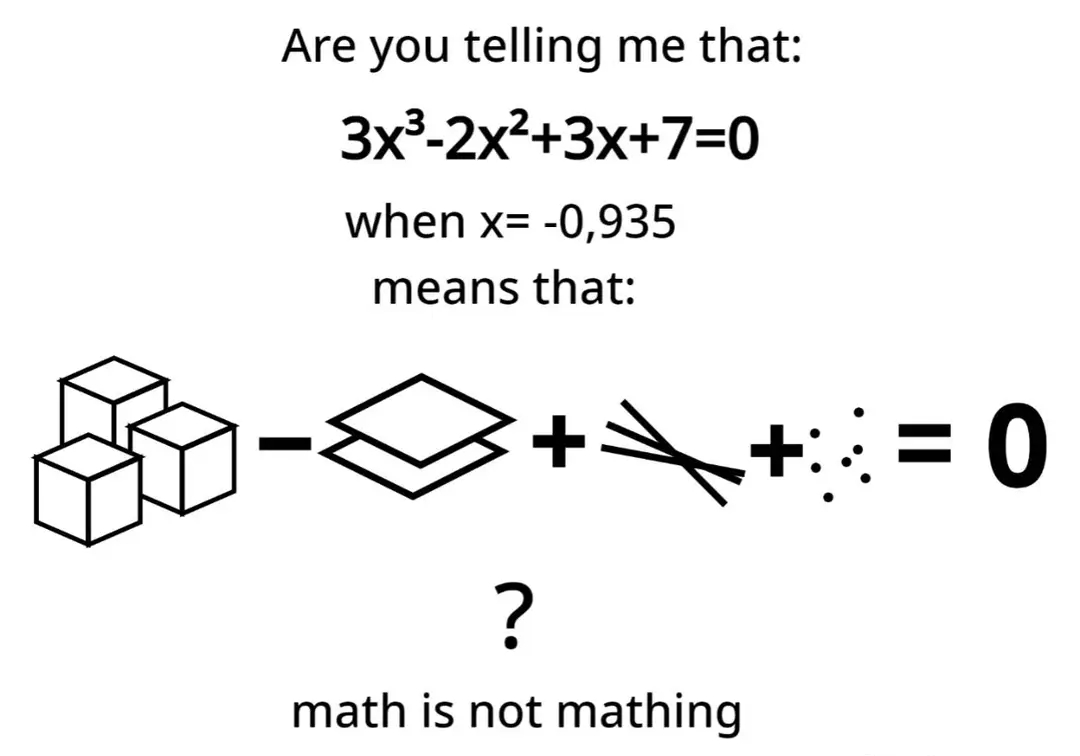Polynomials Memes

The evolution of the Twitter/X logo perfectly mirrors mathematical functions! First we have the linear function (y = mx + b), then the quadratic function (y = x²), and finally the cubic function (y = x³). Elon's rebranding accidentally created a mathematical progression that perfectly represents increasing complexity and higher-order polynomials. Next rebrand will probably be a quartic function with inflection points worthy of a calculus nightmare. The math nerds spotted this correlation before the marketing team did!

When your math problem has a nice clean radical like √x? Mathematicians swoon and call it an "exact solution" despite it being just as approximate as anything else when you calculate it numerically. But dare to present an arbitrary polynomial or trig function as an "exact solution" and suddenly you're getting desperate calls to HR! The hypocrisy! It's mathematical discrimination at its finest—where √2 gets the red carpet treatment while sin(π/7) gets treated like it showed up to a black-tie event wearing sweatpants. Both are irrational numbers that need approximation in practice, but only one gets the mathematical seal of approval!

Ever notice how math problems go from "yeah, I got this" to "I need therapy" with just one tiny change? That's polynomial roots for ya! On the left, we have x³-x with its neat little roots at 0, 1, and -1 — practically begging to be solved. But add that innocent-looking "-1" to get x³-x-1 and suddenly you've entered mathematical horror territory. That equation can't be solved with radicals thanks to Galois theory, which is basically the math world's way of saying "nice try, human." It's like going from making instant ramen to trying to cook a five-course French meal... while blindfolded... on a unicycle. Next time someone says math is straightforward, show them this and watch their soul leave their body.

Calculus nerds have found their ultimate crossover episode! The meme brilliantly pits pop star Taylor Swift against the mathematical Taylor Series, and the results are *infinitely* clear. While Swift might dominate the charts, she can't help you approximate sine functions or reduce those pesky nonlinear equations. Meanwhile, the Taylor Series is out here expanding functions around points like it's no big deal, showing up on your calculus exam, and training your analytical reasoning skills. The Taylor Series (that beautiful summation formula) lets mathematicians approximate complex functions using polynomials - basically the mathematical equivalent of having backup dancers make you look good. Just remember its effectiveness depends on the convergence range, unlike Swift's range which consistently hits those high notes. Next album idea: "Taylor's Version (Expanded Around a Point)"

Behold, the moment when math transcends numbers and becomes hieroglyphics! The polynomial equation is supposedly "solved" by replacing variables with random shapes—cubes, diamonds, sticks, and dots. It's like watching someone try to pay their bills with Monopoly money and expecting the bank to accept it. This is what happens when students who hate algebra create their own solution methods. "Math is not mathing" indeed—it's having an existential crisis. Next time your professor asks for the solution, just draw a bunch of emojis and claim it's advanced mathematical notation from the future.

Behold! The ultimate mathematician's guide to self-pleasure! What mere mortals do with their hands, mathematicians do with formulas! The stick figure's little doodle shows π/2 radians (that's 90 degrees for you non-math types) alongside a polynomial equation. Because nothing says "getting frisky" like converting between coordinate systems and solving for x! The fake book title with "Volume One" implies there's an entire series of these mathematical self-gratification techniques. Those number-crunchers really do find their bliss in the most abstract ways possible! Next time someone says math isn't exciting, show them this—they've clearly been doing their calculations wrong!

This is what happens when mathematicians try to flirt. One character innocently shares a neat formula (the sum of first n odd numbers equals n²), only to get absolutely demolished by a math elitist dropping Pascal's triangle and polynomial summations like they're dropping a mic. The poor kid's soul leaves their body as they realize their "cool math fact" was just the baby pool of mathematical complexity. It's like bringing a calculator to a supercomputer fight. That stunned "Wha-" at the end? That's the universal sound of someone who just wanted to share a fun fact but instead received an existential crisis wrapped in sigma notation.

Every math student's internal monologue: "Is that a binomial I see? Time to FACTORIZE!" The meme perfectly captures that moment when you spot a difference of squares (a²-b²) and your brain automatically splits it into its factored form (a-b)(a+b). It's that satisfying mathematical reflex that makes you feel like you've unlocked a secret power. The factoring instinct is so deeply ingrained that you can't help but mentally distribute those terms faster than you can say "polynomial." Math nerds unite!

The mathematical holy war we didn't know we needed! This bell curve meme brilliantly captures how understanding of polynomials follows the intelligence distribution. The average folks (middle of the curve) are confidently wrong, insisting "a polynomial is NOT a function" with that panicked face. Meanwhile, both the left and right tails—representing either blissfully simple or galaxy-brain intelligence—correctly understand that polynomials are indeed functions. It's the perfect illustration of the Dunning-Kruger effect in math education. The beginners and experts agree, while those with just enough knowledge to be dangerous are busy making angry forum posts about definitions they misunderstood in Algebra II.

The bell curve of mathematical understanding strikes again! On the far left, we have the blissfully clueless folks asking "wtf is a polynomial" with their 55 IQ. In the middle peak at 100 IQ, we have the textbook warriors confidently stating "a polynomial is a function" (they memorized that from Chapter 1). Then on the far right, the 145 IQ galaxy brains declare "a polynomial is NOT a function" before the final enlightened sage corrects them with "erm... actually" – because technically, polynomials are expressions that can be used to define functions, but they aren't functions themselves. It's that beautiful moment when you've gone so deep into math that you circle back to sounding like you don't understand math. The duality of polynomial existence is keeping math professors employed worldwide!

The skeleton lifting weights isn't just building bone density—it's factoring polynomials. Vieta's formulas transform quadratic equations from standard form into factored form without breaking a sweat. Meanwhile, I'm over here using the quadratic formula like a caveman. The true gym bros know: why calculate roots when you can just factor? That's mathematical efficiency at its finest.

Looking for a neat formula to solve quintic equations? Évariste Galois is pointing at you like "Not so fast, buddy!" While we've got cute formulas for quadratics, cubics, and even quartics, Galois Theory crashed the party with a mathematical proof that no general formula exists for polynomials of degree 5 or higher. That's right—mathematicians spent centuries hunting for something that's mathematically impossible! Next time your calculus professor assigns a quintic equation, just write "Galois said no" and drop the mic. (Results may vary, especially during finals.)