Euler's identity Memes

Mathematicians: "Euler's identity (e^(iπ) + 1 = 0) is the most beautiful equation in mathematics!" Euler: "Hold my beer." The meme shows Euler's epic comeback to critics calling his famous identity boring - creating this monstrosity that crams every number from 0-10 and multiple mathematical constants into one completely nonsensical equation. It's basically mathematical flexing taken to ridiculous extremes. The French text even declares it "The true most beautiful equation in the world" which is like calling a toddler's finger painting the next Mona Lisa. Pure mathematical shitposting at its finest!

Math students can never escape the watchful gaze of Leonhard Euler! That's right - the Swiss mathematician who haunts every corner of advanced math like Spider-Man patrols New York. Calculus homework? Euler's there. Number theory? Euler's constant is watching. Trying to solve a topology problem at 2AM? BAM! Euler's formula jumps out of nowhere! The man contributed to practically EVERY field of mathematics - from graph theory to infinitesimal calculus. His legacy is so massive that mathematicians literally can't turn around without bumping into another one of his 500+ theorems or identities. No wonder they see his face everywhere... he basically invented half of modern math!

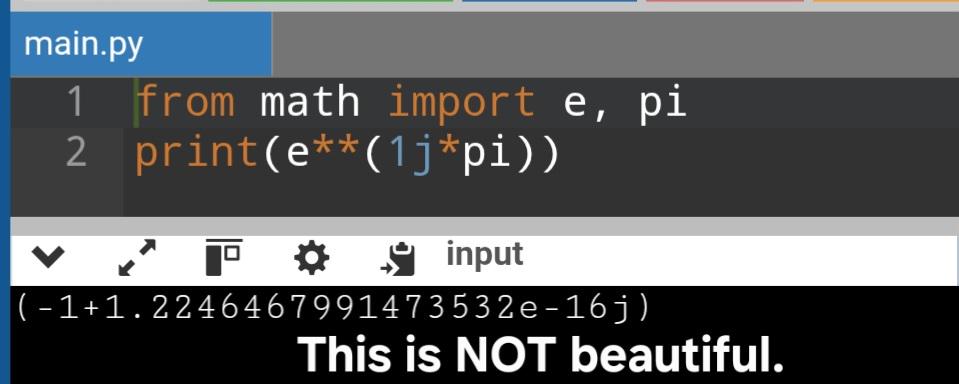
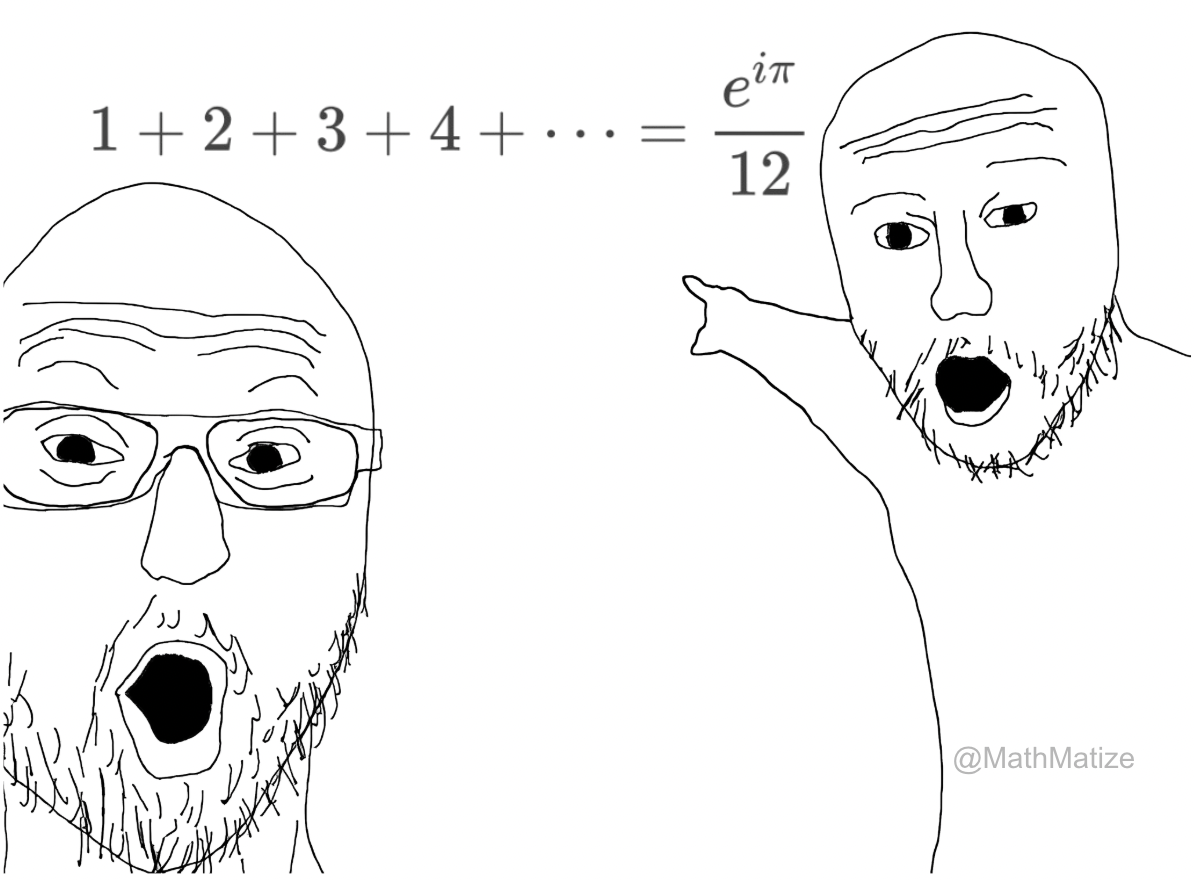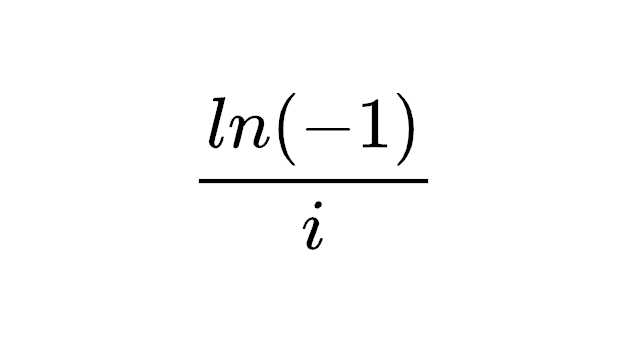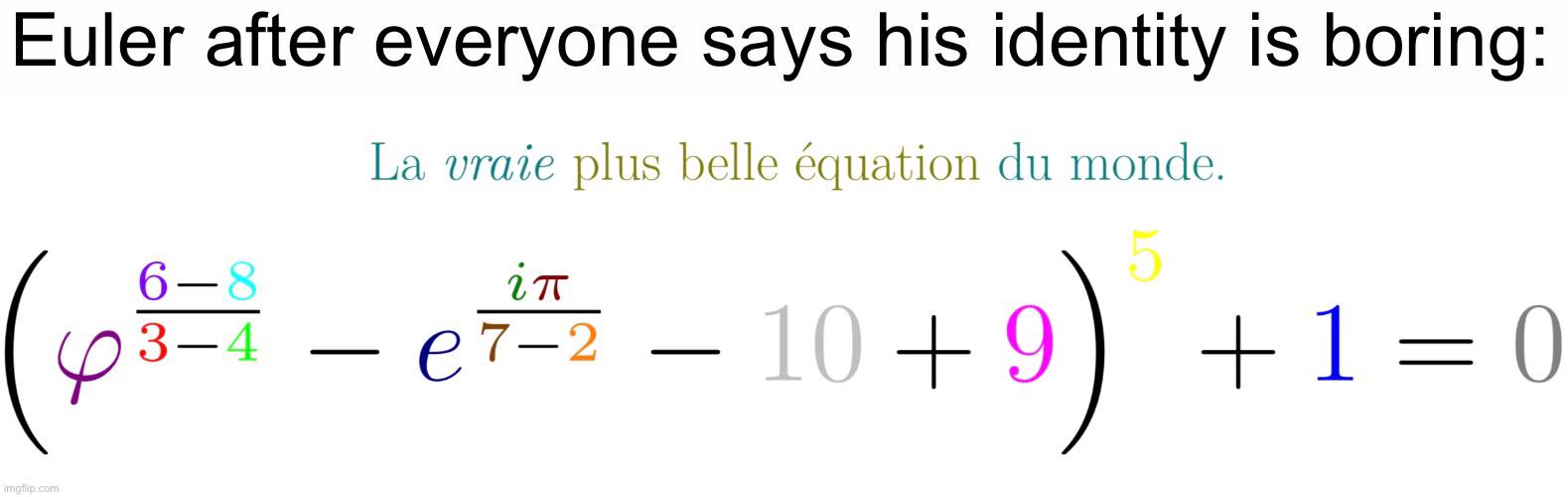Leonhard Euler, the ultimate mathematical hipster who was into formulas before they were cool. That smug expression says it all—he's probably thinking about how he discovered so many mathematical concepts that we're still naming things after him centuries later. Got a fresh new theorem? Sorry buddy, check Euler's 850+ publications first. The man literally has a constant (e), an identity, equations, and even a line named after him. He's basically the mathematical equivalent of "I was into that band before they got famous." Next time you have a mathematical epiphany, just know that Euler is time-traveling from the 1700s to whisper "citation needed" in your ear.

Math just broke this poor stick figure's brain! First, we accept imaginary numbers (n√-1) as valid mathematical constructs despite their "imaginary" nature. Then BAM! Euler's identity (e πi = -1) shows up and completely shatters reality. It's that moment when math goes from "weird but I'll accept it" to "WHAT SORCERY IS THIS?!" Euler's identity connects five fundamental constants (0, 1, π, e, and i) in one elegant equation that feels like the universe is playing a cosmic prank on us. The stick figure's existential crisis is every math student who suddenly realizes numbers are both completely made up AND eerily perfect at describing our universe. Mathematical gaslighting at its finest!

The meme brilliantly captures the moment of mathematical enlightenment when you realize Euler's identity (e iπ + 1 = 0) can be rearranged into e iπ = -1, and then— gasp —that means e iπ equals the square root of negative one! It's that mind-blowing moment when you connect complex numbers, exponentials, and π in one elegant equation. The character's progression from confusion to shock to absolute revelation perfectly mirrors every math student's journey through complex analysis. This is basically mathematical poetry that makes mathematicians weak at the knees.

The mathematical horror story in two panels! That moment when you realize Euler's identity (e iπ = -1) is correct, but then someone tries to "simplify" it with a square root and creates a mathematical abomination. The cartoon character's progression from confidence to confusion is basically every math student hitting that point in the semester where elegant equations suddenly transform into eldritch horrors. The square root of negative one is already imaginary—we don't need to make it extra imaginary by butchering beautiful equations!

Poor John Venn, forever in Euler's shadow. The mathematical equivalent of showing up to a party where someone already claimed all the good snacks. Leonhard Euler was the original academic credit hog—the guy published over 900 papers and still wanted the diagrams too! At this point, mathematicians should just rename the field "Eulermetrics" and call it a day. What's next? Breathing becomes "Euler respiration"? The sun is now "Euler's light source"? The ultimate mathematical power move isn't solving equations—it's getting your name stamped on everything like some 18th-century Swiss branding genius.

The character's escalating confusion perfectly mirrors every math student's journey through Euler's identity. First panel: "Oh, that's a neat equation." Second panel: "Wait, so e raised to imaginary pi equals negative one? That's... strange." Third panel: "HOLD UP. Are you telling me the exponential function equals the square root of a negative number?!" This is why mathematicians have that thousand-yard stare. They've seen things. Imaginary things. In the complex plane.

The top row shows the mathematical royalty - 0, 1, i, π, and e - looking all smug in their red outfits. But the real mathematical magic happens below with Euler's Identity: e iπ + 1 = 0. This equation is basically the mathematical equivalent of finding out all your favorite celebrities are secretly related. It elegantly connects five fundamental constants in one tight little package, and mathematicians absolutely lose their minds over it. Richard Feynman called it "the most remarkable formula in mathematics." The rest of us just nod and pretend we fully appreciate its profound beauty while secretly wondering if we can use it to calculate our grocery bills. (Spoiler: you cannot.) What makes it truly spectacular is how these seemingly unrelated numbers from different mathematical neighborhoods—an irrational transcendental number (e), an imaginary unit (i), another irrational transcendental number (π), and the most basic integers (1 and 0)—somehow form a perfect equation. It's like discovering your pet goldfish, your car keys, your existential dread, and that sock you lost in 2018 are all secretly part of one cosmic conspiracy.