Complex analysis Memes

The bell curve of mathematical sophistication in its natural habitat. On the left, the blissfully simple "π=3.14" crowd—good enough for high school physics and calculating how much pizza to order. In the middle, the panicked "π≈22/7" users—undergraduate students having their first existential crisis about rational approximations. And on the right, the ominous "π=ln(-1)÷iota" crowd who've gone so deep into complex analysis they've emerged with a concerning level of confidence and a suspicious hoodie. Meanwhile, the true mathematical sweet spot—355/113—sits neglected, offering six decimal places of accuracy while requiring minimal effort. The duality of pi approximations: either too simple to be useful or so complex they're basically showing off.

The Riemann zeta function looking like a mathematical supermodel on its polar graph. Those curves are so elegant they'd make Euler weep. Mathematicians spend decades trying to prove the Riemann Hypothesis while the rest of us are just here admiring how it looks like a fancy audio equalizer. The mathematical equivalent of posting thirst traps on Instagram – no wonder they used fire emojis in the title.

Oh sweet summer child who thought math was "boring"! The meme shows someone fleeing from the mathematical madness that awaits beyond first-year courses. First-year math is just "2+2=4" kindergarten stuff compared to the Klein bottles, complex integrals, and Euler's identity waiting to devour your sanity in advanced mathematics! It's like saying "I stopped watching horror movies because they weren't scary" right before Cthulhu himself kicks down your door with differential equations in one tentacle and non-Euclidean geometry in the other. The mathematical grim reaper is coming for you, and he's armed with more symbols than your keyboard has keys!

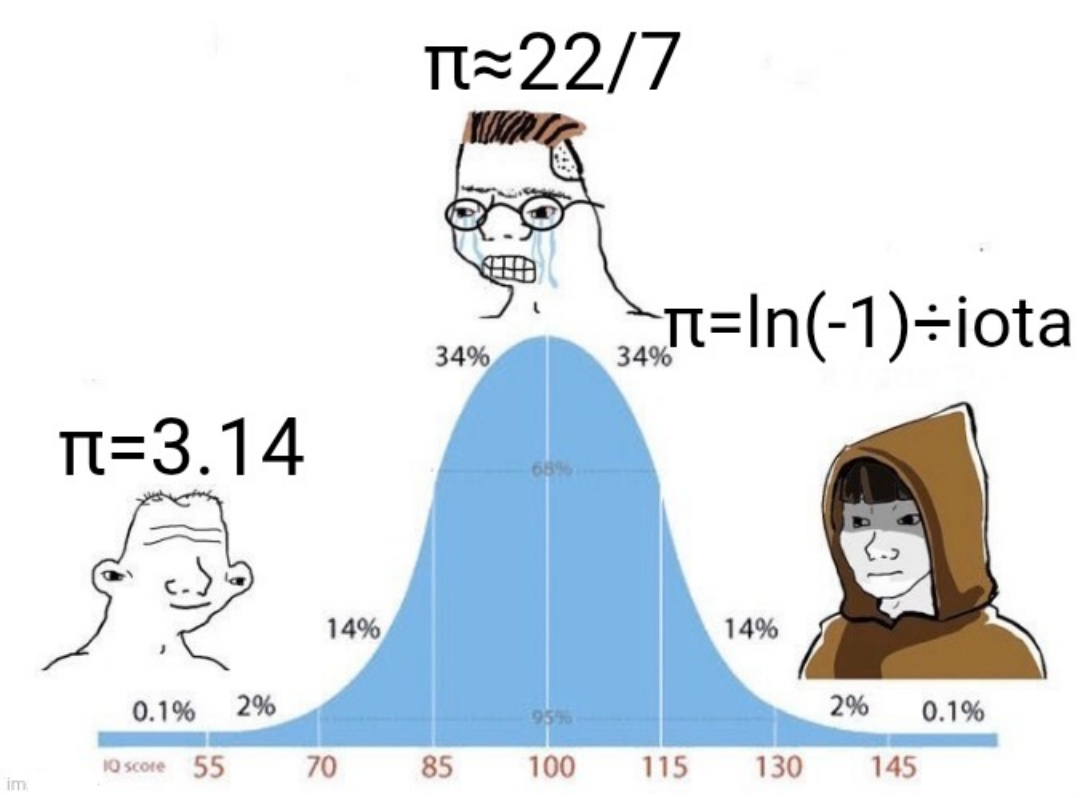
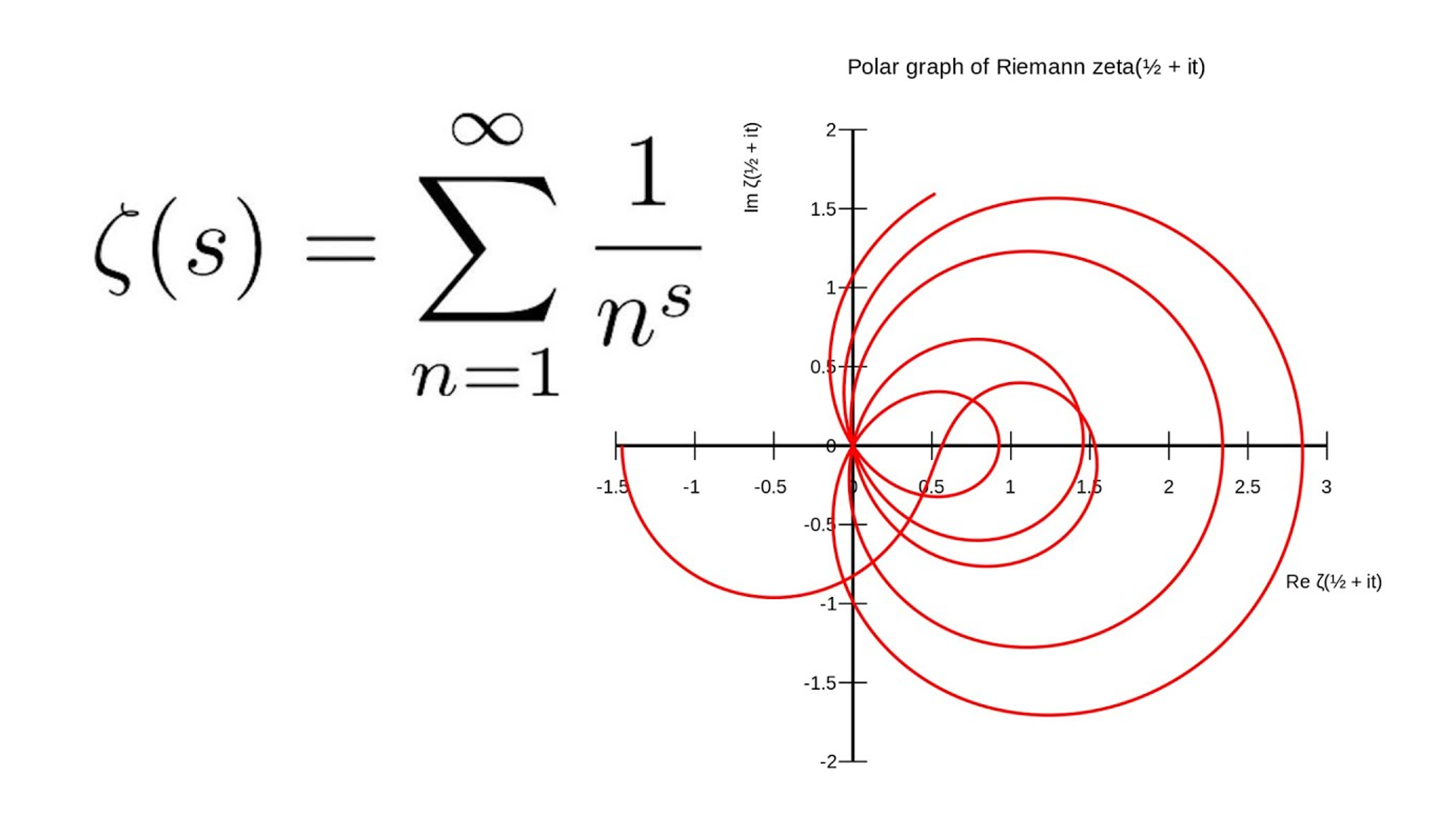
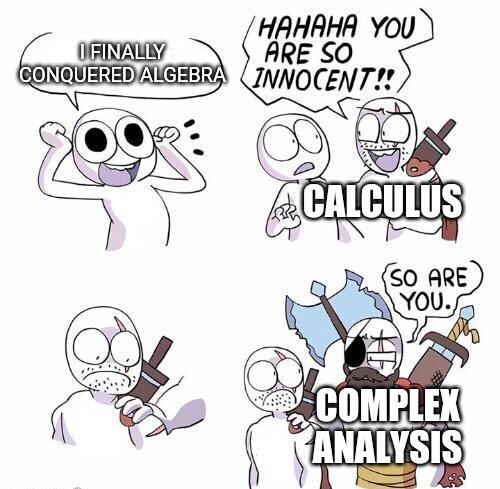
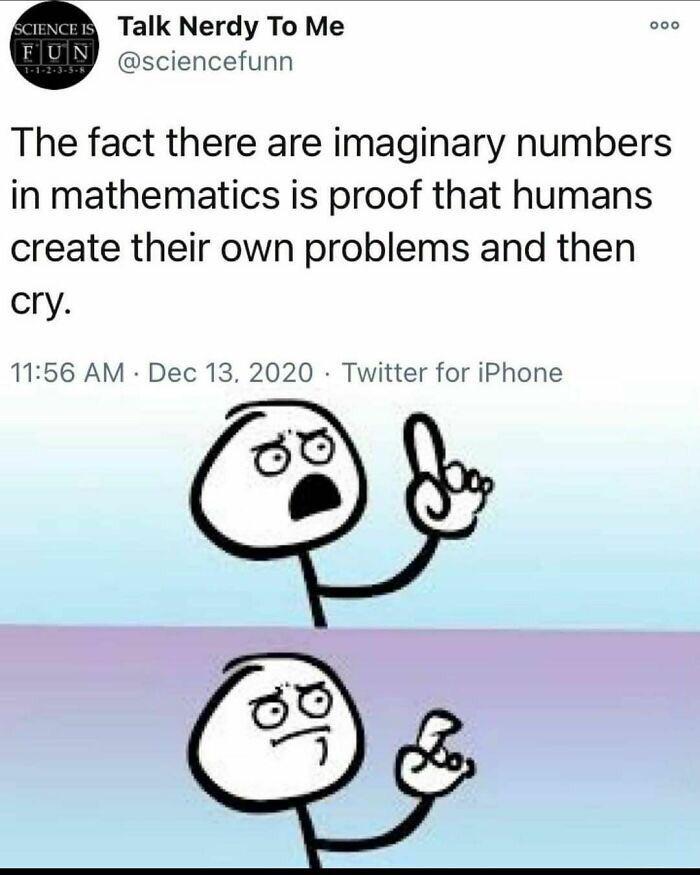
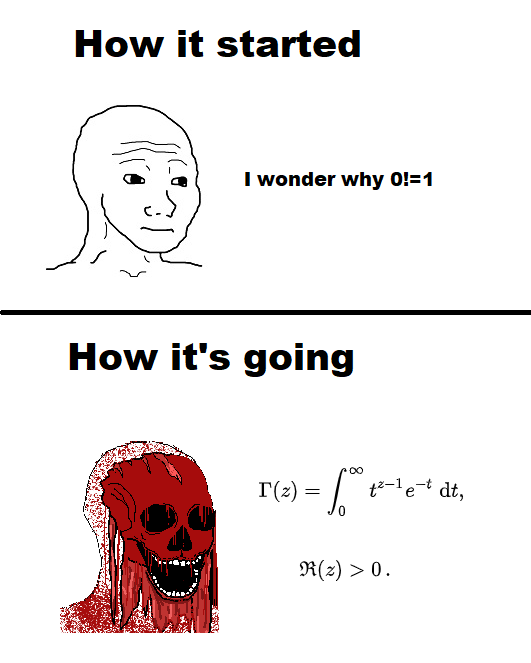
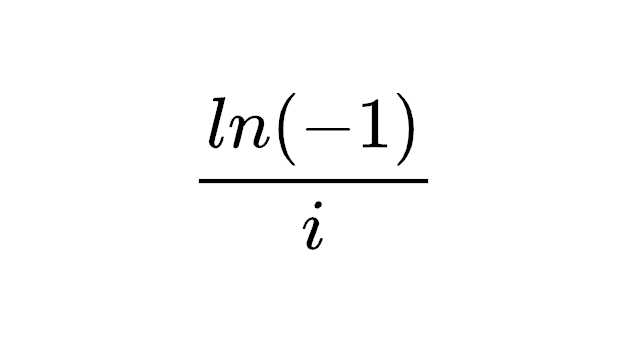Ever notice how math proofs start with elegant formulas and end with "...and the rest is left as an exercise for the reader"? This meme captures that mathematical breaking point perfectly! The proof begins with Johann Bernoulli's complex identity, continues with some fancy integration, then suddenly hits the red box of truth: "Bernoulli, however, did not evaluate the integral." Translation: even the great mathematicians sometimes said "you know what, I'm done here." Next time your professor assigns homework with "trivial" steps, remember that even Bernoulli had his limits!

The mathematical trickery here is absolutely brilliant! This expression ln(-1)/i actually equals π! Why? Because ln(-1) equals iπ in complex analysis (since e iπ = -1 ). So we have (iπ)/i , and the i 's cancel out, leaving us with π! It's like pulling a mathematical rabbit out of a hat that only the cool kids in the complex plane understand. Next time you forget π, just casually scribble this down and watch your math professor either nod approvingly or have an existential crisis.

The mathematical hierarchy of suffering is beautifully captured here. Just when you think you've mastered algebra and life is good, calculus shows up with a baseball bat to humble you. And right when you've nursed those wounds and conquered calculus? Complex analysis appears, armed and dangerous, to remind you that mathematical trauma is an infinite series that never converges. The real joke is on anyone who thinks there's an endpoint to mathematical pain. Linear algebra, differential equations, and topology are just waiting in the shadows, sharpening their weapons.

Mathematicians literally invented an entire number system just because they couldn't handle the square root of negative numbers. "Oh no, √-1 breaks our rules! Let's call it i and build a whole new dimension of mathematics!" Then they spent centuries developing complex analysis, only to have existential crises when their equations produced results that couldn't exist in our physical reality. The ultimate self-inflicted mathematical trauma. Next time you're stressed about your problems, remember that somewhere a mathematician is sobbing over numbers they made up themselves.

What starts as an innocent question about why 0! equals 1 quickly spirals into the mathematical abyss of the gamma function. The top panel shows our naive beginning—just a curious mind pondering factorial basics. The bottom panel reveals the mathematical horror show that follows, complete with complex integrals and conditions on the real part of z. This is the mathematical equivalent of opening Wikipedia to look up a simple fact and finding yourself, three hours later, reading about obscure Romanian folk dances. The gamma function is essentially the factorial function's evil twin that works for non-integer values, and once you start trying to understand it, your brain turns into that screaming skull. The definition shown (Γ(z) = ∫₀^∞ t^(z-1)e^(-t) dt) is what mathematicians call "elegant." The rest of us call it "the reason we switched majors."

This is what happens when mathematicians try to flex their dating skills! The meme brilliantly disguises a profanity as the result of a complex calculus problem. Starting with intimidating complex analysis (contour integrals and residue theorems), the proof cleverly manipulates variables b , i , t , c , h , and e s to spell out a certain word. The punchline that "bitches can be integrated, but they are complex" is pure mathematical wordplay genius. It's the perfect blend of advanced math and college humor that would make even Euler snort coffee through his nose!

The mathematical glow-up we all dream about! In real analysis, you're stuck staring at an impossible-looking integral with no clear path forward. But switch to complex analysis, and suddenly you're transforming integrals with contour integration and residue theory like a mathematical wizard. This is basically the math equivalent of learning that one weird trick doctors hate. Regular calculus has you sweating bullets, while complex analysis lets you smugly call the same problem "trivial" after applying some residue magic. It's like discovering you can solve puzzles by simply stepping into another dimension!

The classic trolley problem just got a mathematical nightmare upgrade! Instead of a simple moral dilemma, now you're facing the Riemann zeta function—one of math's most notorious unsolved puzzles. You'd need to solve where ζ(s)=0 for complex values (those pesky zeros that mathematicians have been hunting for centuries)! Even the greatest mathematical minds would freeze at the lever, paralyzed by the impossible proof. Suddenly, letting the trolley take its natural course seems like the easier option! The ultimate mathematician's horror story—when ethics requires solving the unsolvable.

Remember when math was just cute little factorials? Then one day you turn around and BAM—your shadow has morphed into the gamma function integral! That's the mathematical equivalent of finding out Santa isn't real. One minute you're happily computing 5! = 120, and the next you're staring into the abyss of complex analysis wondering where your childhood went. The factorial's evil twin doesn't just calculate non-integer factorials—it calculates your descent into mathematical madness!